Предмет: Алгебра,
автор: MrPerelman
Срочно!! Решите логарифмическое неравенство много баллов.
Приложения:
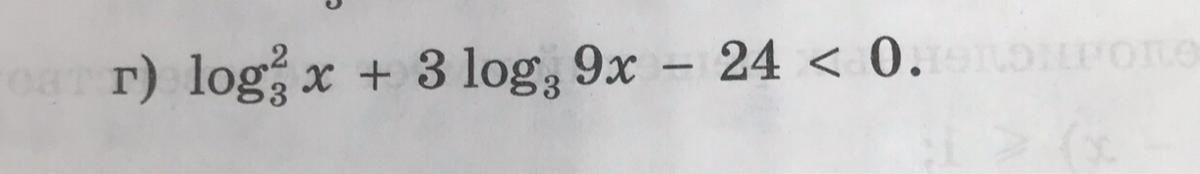
Ответы
Автор ответа:
1
Ответ:
х ∈ (1/729; 27)
Объяснение:
log₃²(x) + 3log₃ (9 · x) - 24 < 0 ОДЗ: x > 0
log₃²(x) + 3log₃ (9) + 3log₃(x) - 24 < 0
log₃²(x) + 3 · 2 + 3log₃(x) - 24 < 0
log₃²(x) + 3log₃(x) - 18 < 0
Замена t = log₃(x)
t² + 3t - 18 < 0
Находим корни уравнения t² + 3t - 18 = 0
D = 9 + 72 = 81
t₁ = (- 3 - 9)/2 = -6
t₂ = (- 3 + 9)/2 = 3
Применяем метод интервалов
Знаки t показаны на числовой прямой
-------- + -------- -6------------ - -------------------------- 3 --------- + -------
Решение неравенства t² + 3t - 18 < 0 имеет вид t∈(-6; 3)
Возвращаемся к замене
1) log₃(x) = - 6
3⁻⁶ = х
х = 1/729
2) log₃(x) = 3
3³ = х
х = 27
х ∈ (1/729; 27)
braveman90:
небольшое замечание или даже скорей совет, что если мы находим ОДЗ, то в итоге ожидаем увидеть координатную ось конечную с нанесенной на нее ОДЗ...в остальном идеально (=
Автор ответа:
1
Ответ:
x ∈ (; 27)
Объяснение:
все решение представлено на фотографии.
Приложения:
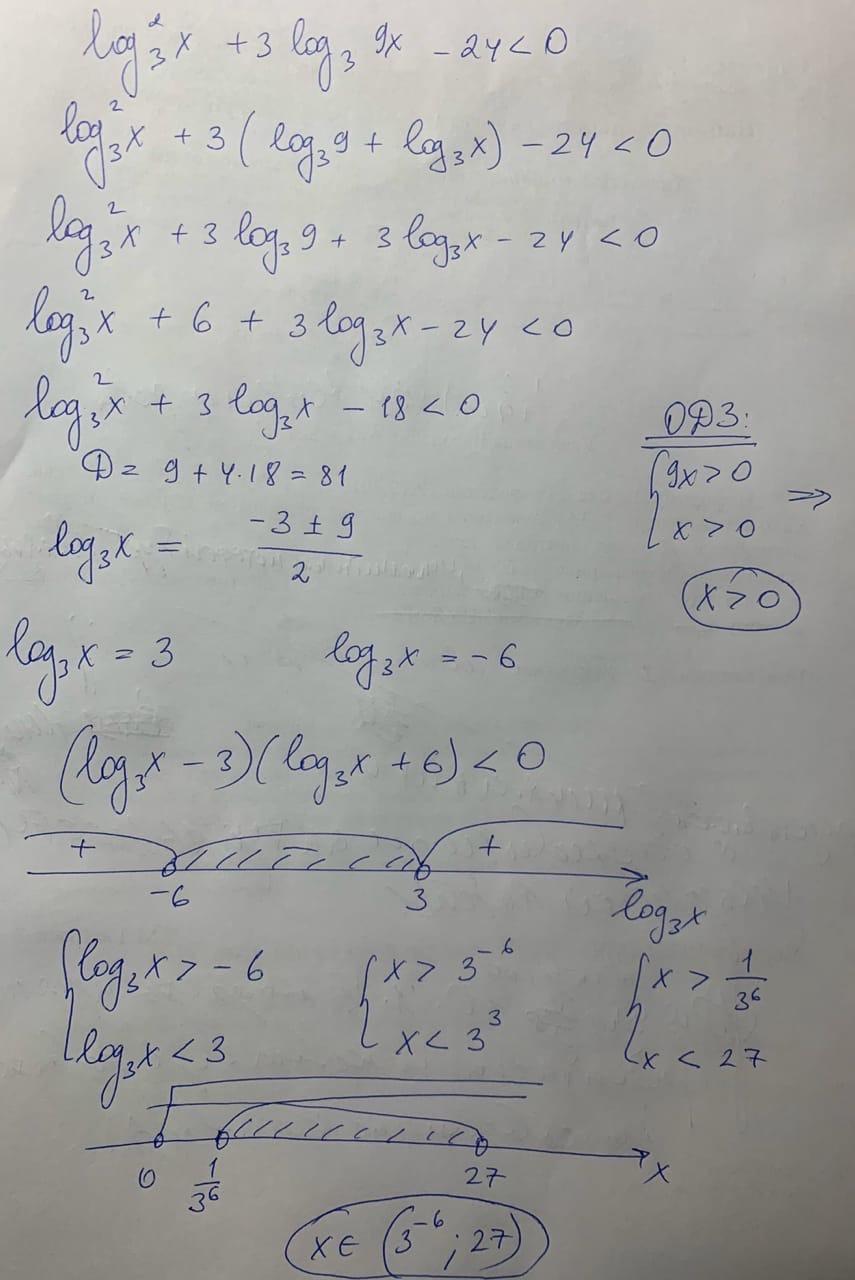
Похожие вопросы
Предмет: Английский язык,
автор: loshka34354
Предмет: Українська мова,
автор: zcazcaf2
Предмет: История,
автор: yanabarret7
Предмет: Математика,
автор: русский132