Предмет: Алгебра,
автор: Mr0leg
Вычислить производную, №5
Приложения:
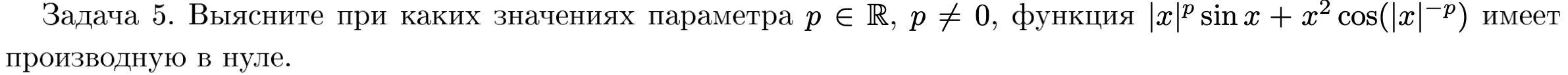
Ответы
Автор ответа:
3
Ответ:
при p > 0
Объяснение:
Если функция дифференцируема в нуле, то она и непрерывна.
Функция разрывна при и потому при таких p не имеет производной.
Положим p > -1. По определению, производная в точке 0 будет существовать, если существует и конечен предел
При -1 < p < 0 предел не является конечным, производной не существует. При p > 0 производная существует (и равна нулю)
Похожие вопросы
Предмет: Алгебра,
автор: sofiavanovic5
Предмет: Математика,
автор: egorhyrzhiy
Предмет: История,
автор: gorbalroman8
Предмет: Алгебра,
автор: romanaz1337
Предмет: Математика,
автор: шайх