Предмет: Алгебра,
автор: Mr0leg
Вычислить производную, №4
Приложения:
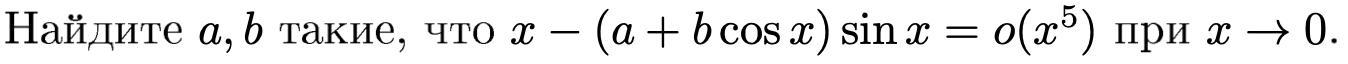
Ответы
Автор ответа:
3
Раскладываем в ряд Тейлора:
Все коэффициенты в скобках должны обнулиться. Очевидно, такое невозможно: коэффициенты при третьей и пятой степени одновременно нули, только если a = b = 0, но тогда коэффициент при x равен 1.
Если требуется найти a и b такие, что или
, то достаточно требовать обнуления коэффициентов при первой и третьей степенях. Это будет выполнено, если a = 4/3, b = -1/3.
Похожие вопросы
Предмет: Алгебра,
автор: danyamig
Предмет: Українська мова,
автор: maksimpro2283
Предмет: Литература,
автор: oleksandrasajtan
Предмет: Обществознание,
автор: ruslan4444455
Предмет: Физика,
автор: DianaIlinitskaja