Предмет: Алгебра,
автор: Lana2201
Упростить выражение
Заранее спасибо :)
Приложения:
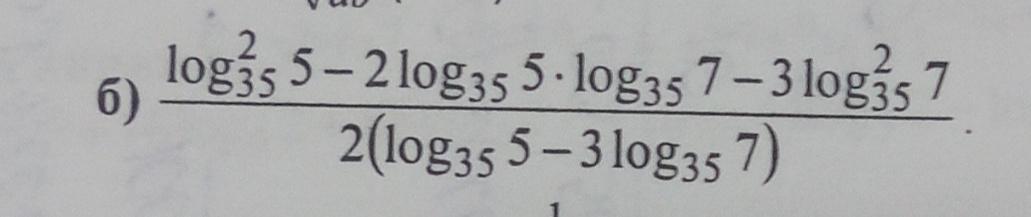
Ответы
Автор ответа:
1
Ответ:
0.5
Объяснение:
Похожие вопросы
Предмет: Математика,
автор: vladalukomskaa2
Предмет: Математика,
автор: anzelalutsuk3
Предмет: Химия,
автор: polahdavid28
Предмет: Литература,
автор: docha2016ksyunya
Предмет: Математика,
автор: Evysja