Question

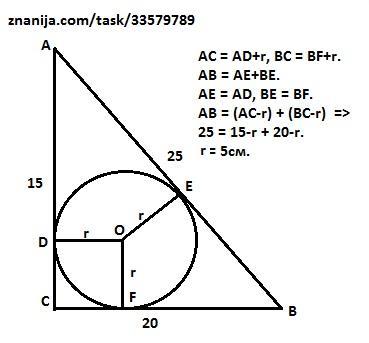
Найдите радиус окружности, вписанный в прямоугольный треугольник если гипотенуза равна 25 см, а один из катетов - 20 см.

Answer 1

Ответ:

R=5 см.

Объяснение:

Второй катет b²=с²-а²=625-400=225; b=√225=15.

Радиус равен R=(а+b-с)/2=(15+20-25+/2=5

Answer 2

Ответ:

r = 5 см

Объяснение:

Второй катет этого треугольника равен 15 см, так как треугольник пифагоров (или египетский).

Точки касания вписанной окружности делят стороны так, что

25 = (15-х) + (20-х)  =>  х = 5 см. (касательные их одной точки равны).