Предмет: Алгебра,
автор: kjuliyaa
Найти все решение уравнения (фото приложено). Тема- комплексные числа.
Приложения:
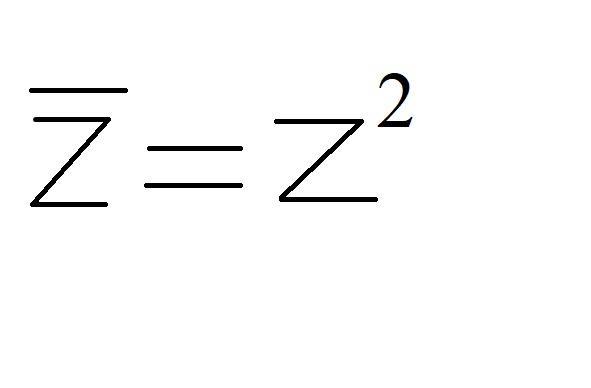
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Нам нужно найти все комплексные числа, квадрат которых равен их сопряжённому числу.
Пусть
искомое число.
Тогда его сопряжённое число
По условию задачи:
Подставим вместо комплексных чисел их представления через действительные x и y. Получим:
Преобразуем:
Два комплексных числа равны, когда равны соответственно их действительные и мнимые части:
Рассмотрим второе уравнение в системе:
Если y = 0, то
Если x = -0.5, то
В итоге получаем, что
Похожие вопросы
Предмет: Математика,
автор: ksusakorol244
Предмет: Другие предметы,
автор: zelencukveronika
Предмет: Математика,
автор: oleksandrbutok
Предмет: Математика,
автор: Nik2006k
Предмет: Химия,
автор: IluaSud