Предмет: Геометрия,
автор: Аноним
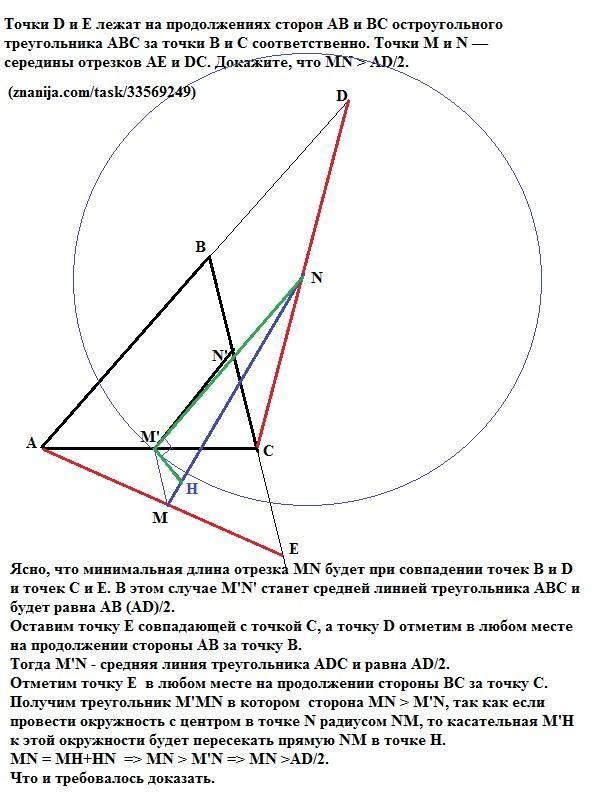
Точки D и E лежат на продолжениях сторон AB и BC остроугольного
треугольника ABC за точки B и C соответственно. Точки M и N — середины
отрезков AE и DC. Докажите, что MN > AD/2.
Ответы
Автор ответа:
1
Ответ:
Доказательство в объяснении.
Объяснение:
Ясно, что минимальная длина отрезка MN будет при совпадении точек B и D и точек С и Е. В этом случае M'N' станет средней линией треугольника АВС и будет равна AB (AD)/2.
Оставим точку Е совпадающей с точкой С, а точку D отметим в любом месте на продолжении стороны АВ за точку В.
Тогда M'N - средняя линия треугольника АDC и равна AD/2.
Отметим точку Е в любом месте на продолжении стороны ВС за точку С. Получим треугольник M'MN в котором сторона MN > M'N, так как если провести окружность с центром в точке N радиусом NM', то касательная M'H к этой окружности будет пересекать прямую MN в точке Н.
MN = MH+HN =>
MN >(M'N = AD/2)
=> MN >AD/2.
Что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: rekit4921
Предмет: Українська мова,
автор: Аноним
Предмет: Химия,
автор: angelinaguk4
Предмет: Математика,
автор: coolaru1
Предмет: Алгебра,
автор: WalruscatArnie