Предмет: Алгебра,
автор: nataKross
Решите пожалуйста!
Срочно!
Приложения:
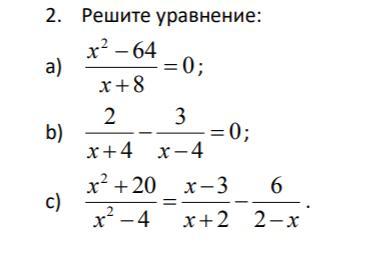
nataKross:
желательно подробно
Ответы
Автор ответа:
1
Ответ:
Объяснение:
a) x^2 = 64 => x = 8; -8. Но так как x -8 (потому что тогда знаменатель будет 0, а такого допускать нельзя), то ответ - x = 8.
b) Приводим к общему знаменателю и приравниваем числитель к 0.
Сразу записываю числитель. -x - 20 = 0 => x = -20. x 4; -4. Ответ x = -20
c) Тоже приводим всё к общему знаменателю и приравниваем числитель к 0. Только запишем дробь -6/(2-x) вот так: 6/(x-2).
x^2 + 20 = x^2 + x + 18
x = 2. x -2; 2. Ответ: решений нет.
Автор ответа:
0
Ответ:
а)
b)
c)
Похожие вопросы
Предмет: Математика,
автор: khrystynkapro12k
Предмет: Английский язык,
автор: doliadaria12
Предмет: Английский язык,
автор: ventimpact1208
Предмет: Алгебра,
автор: res234
Предмет: Алгебра,
автор: Sapozhinsky