Question

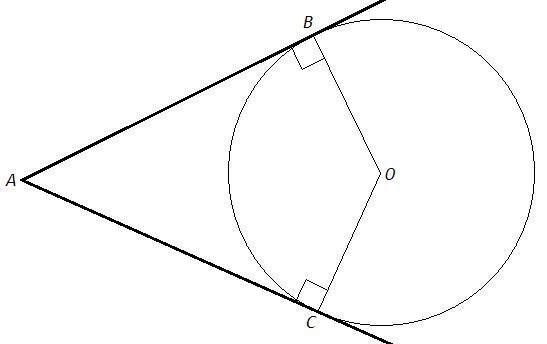
1) Из точки A, которая лежит вне окружности с центром в точке O, проведены касательные AB и AC к этой окружности (B и C - точки касания). Доказать, что четырехтреугольник ABOC можно вписать в окружность.

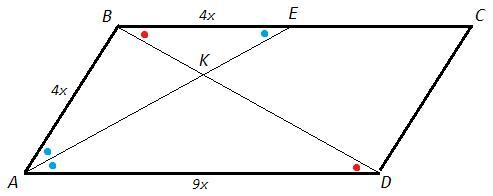
2) В параллелограмме ABCD AE - биссектриса угла А. Стороны параллелограмма AB и BC относятся как 4:9. AE пересекает диагональ BD в точке К. Найти отношения BK:KD (рисунок в изображение) ​

Answer 1

1) Радиус, проведенный в точку касания, перпендикулярен касательной. ABO=ACO=90. Четырехугольник ABOC можно вписать в окружность, так как сумма его противоположных углов равна 180.

2) BAE=DAE (AE - биссектриса)

BEA=DAE (накрест лежащие при BC||AD)

BAE=BEA => △ABE - равнобедренный, AB=BE

BC=AD (противоположные стороны параллелограмма)

AB/BC =BE/AD =4/9

△BKE~△DKA (по накрест лежащим углам при BC||AD)

BK/KD =BE/AD =4/9

Answer 2

Ответ: во вложении Объяснение: