Question

Условие и вопрос на рисунке!!!

Answer 1

Ответ:

Пошаговое объяснение:

Я не буду доводить до ответа, а вот сложную ( с моей точки зрения) часть расскажу.

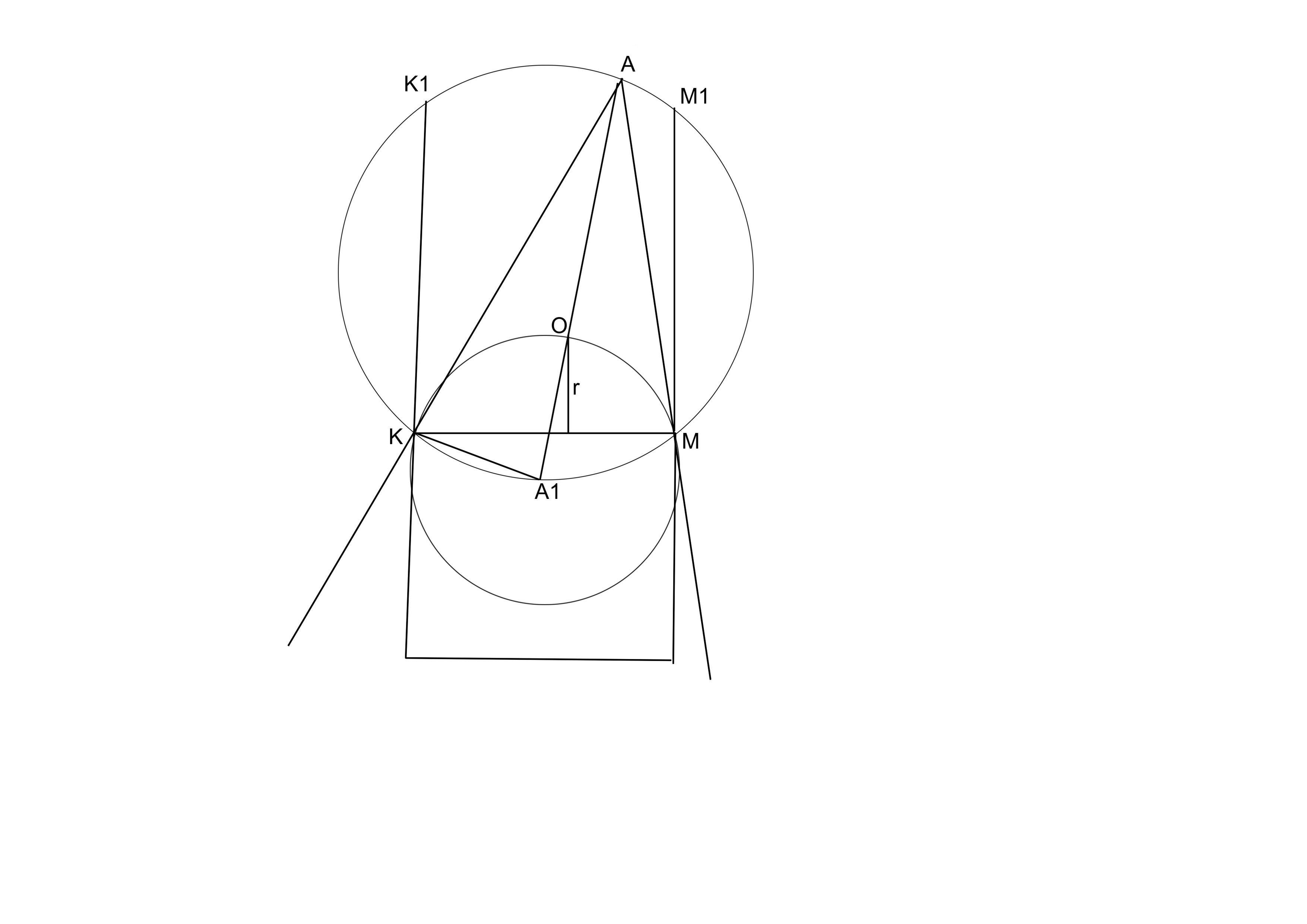
Для начала я заменю эту задачу - другой. Я фиксирую сторону квадрата. тогда получится что-то вроде - смотри чертеж.

Угол A равен 30 градусам, геометрическое место точек A - окружность. При этом квадрат должен находиться внутри угла, поэтому точка A может находиться только на дуге K1M1 этой окружности.

Теперь я задаю такой вопрос - если длина KM фиксирована, какой радиус вписанной в тр-к KMA окружности будет минимальным (если точка А занимает положение на дуге K1M1)?

Центр O вписанной в KMA окружности лежит на биссектрисе AA1, где точка A1 лежит на окружности, описанной вокруг KMA (той самой, по которой бегает точка А, но - в середине нижней дуги KM).

Здесь я сошлюсь на известную задачу, согласно которой A1K = A1M = A1O; доказать это очень просто, рассматривая углы треугольника KOA1, как вписанные углы, и учитывая, что KO - тоже биссектриса. Там получается, что углы OKA1 и KOA1 равны сумме половин углов K и A тр-ка KMA.

Я решил добавить точное доказательство этого факта, поскольку он довольно сложный для восприятия, малоизвестный и полезный.

<KOA1 = <OKA + <KAO = <K/2 + <A/2;

<OKA1 = <K/2 + <MKA1 = <K/2 +<MAA1 = <K/2 + <A/2;

Поэтому треугольник KA1O - равнобедренный, и A1K = A1O;

Уже ясно, что при различных положениях точки A точка O перемещается по окружности с центром в точке A1 и радиусом A1K. Минимальное расстояние до KM будет, если точка A совпадает с M1 (или K1).

Дальше все очевидно. переходя к исходной задаче, надо просто найти катет против угла в 30 градусов в прямоугольном тр-ке с радиусом вписанной окружности 5.

Ну это вы уж сами :).