Предмет: Алгебра,
автор: Detfor
Найти все а, при каждом из которых уравнение |x-a|-|2x+2|=3 имеет единственное решение.
Ответы
Автор ответа:
1
Почему я так смело возводил в квадрат? Если заметить ,то правая часть всегда неотрицательная ,а значит могу возводить и не наносить ограничения
Я привёл данную функцию к двум простейшим ,разберём их
Первая функция!
Мы знаем как выглядит модуль |2x+2| ,но мы его подняли ,а значит его вершина будет иметь координаты (-1;3)
Нам нужно одно решение с прямой x-a
Единственное решение может иметь только тогда ,когда прямая x-a касается вершины,то есть ,подставим вместо x=-1
Получаем:-1-a=3⇔-a=4⇔a=-4
Рассмотрим вторую функцию!
Если заметить ,то можно понять ,что вторая функция симметрична первой ,а значит её вершина будет иметь (-1;-3)
Делаем всё тоже самое ,подставляем x=-1
-1-a=-3⇔-a=-2⇔a=2
При а={-4;2} - будет единственное решение
Приложения:
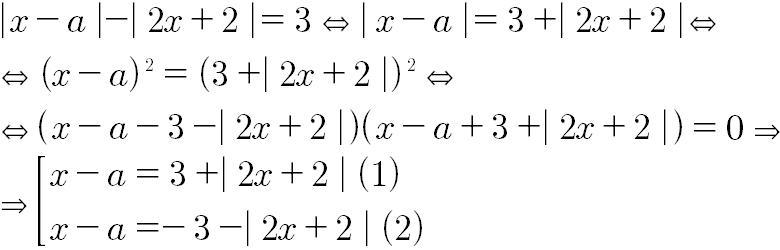
Похожие вопросы
Предмет: Математика,
автор: artempapivnic
Предмет: Математика,
автор: danasevcova0506
Предмет: География,
автор: hfggfdddd
Предмет: Алгебра,
автор: naconechniyleo
Предмет: История,
автор: Аноним