Помогите)
Дан треугольник со сторонами, равными 7 см, 6 см, 5 см.
Постройте треугольник, гомотетичный данному, с центром гомо-
тетии в точке пересечения его медиан и коэффициентом гомотетии, равным:-0,5. Сравните соответствующие углы данного и построенных треугольников.
Ответы
Объяснение:
Дано: АВ = 7 см; АС = 6 см; СВ = 5 см.
Центр гомотетии О - точка пересечения медиан.
Коэффициент гомотетии k = -0,5.
Построить треугольник, гомотетичный данному.
Построение:
Построим ΔАВС.
Начертим отрезок АВ=7 см. Из точки А проведем дугу радиусом 6 см, а из точки В - радиусом 5 см. На пересечении дуг поставим точку С.
ΔАВС - исходный треугольник.
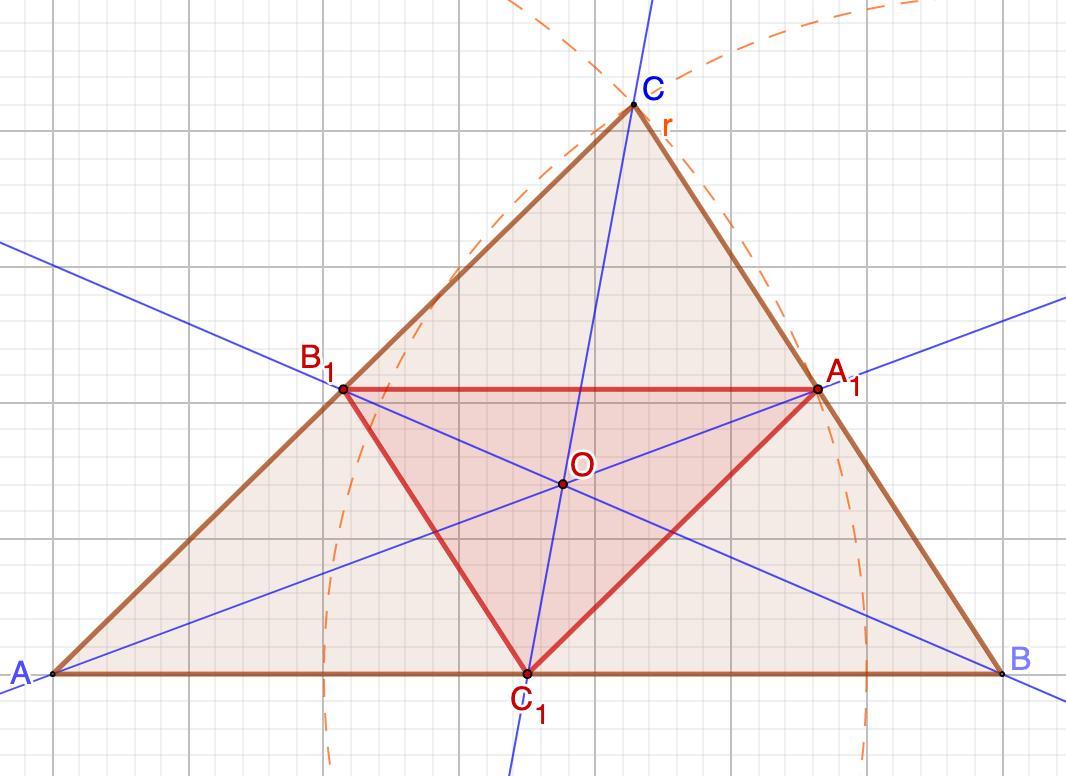
Проведем медианы, пересечение их - точка О - центр гомотетии.
Проведем прямые, соединяющий точку О и вершины ΔАВС.
Так как коэффициент k = -0,5, то ОС₁ = k·ОС=-0,5·OC. Знак минус показывает, что точка С₁ лежит по другую сторону от точки О.
Измеряем ОС и половину длины этого отрезка откладываем от точки О в противоположном направлении. Получаем точку С₁.
Аналогично строим точки А₁ и В₁.
Так как медианы точкой пересечения делятся в отношении 2:1, начиная от вершины. то искомые вершины треугольника А₁В₁С₁ будут находиться на сторонах ΔАВС.
Так как стороны ΔА₁В₁С₁ - средние линии ΔАВС, то они равны половинам его сторон. То есть стороны пропорциональны. ⇒ ΔA₁B₁C₁~ΔABC.
⇒ углы равны.