Решить неравенство с модулем
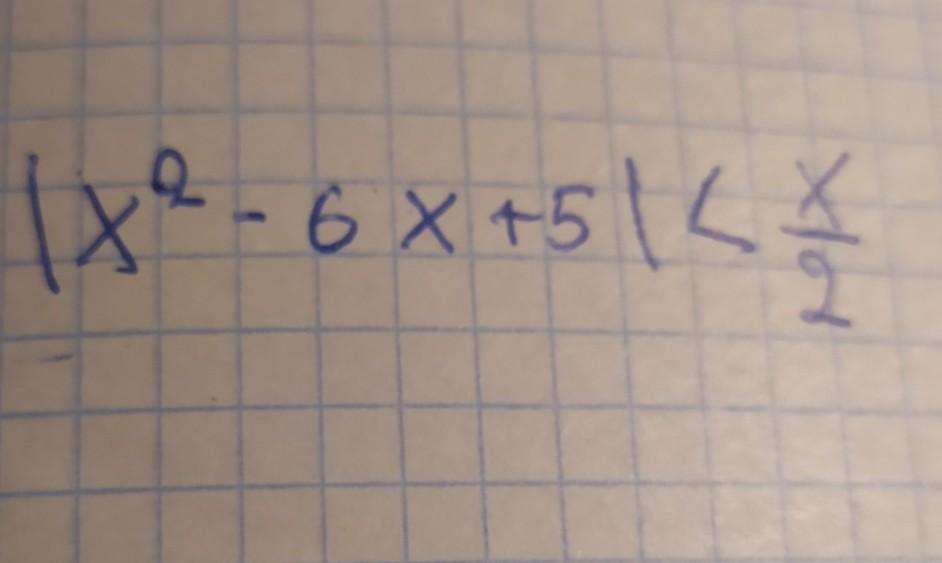
Ответы
Объяснение:
решение на фото сверху
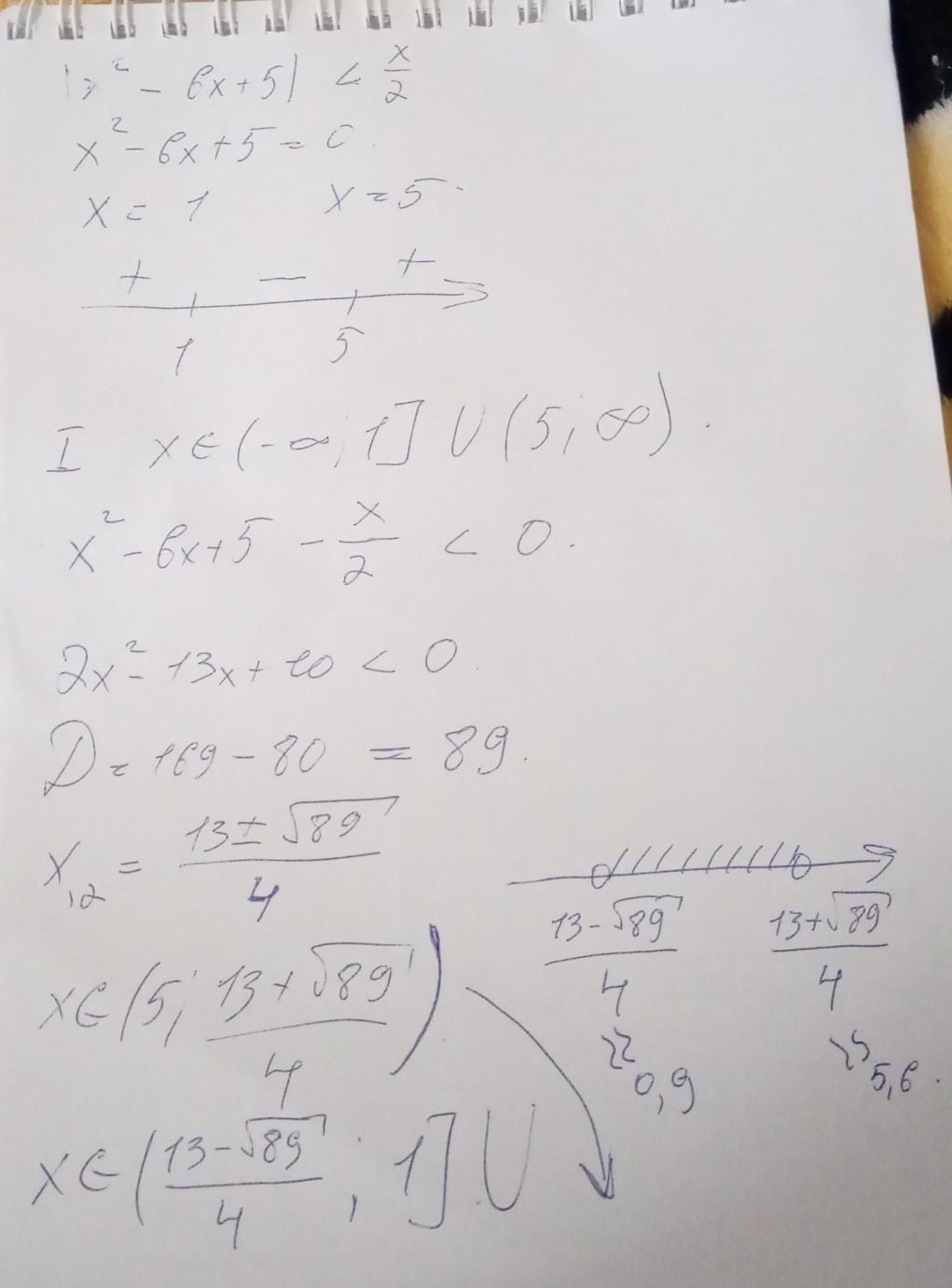

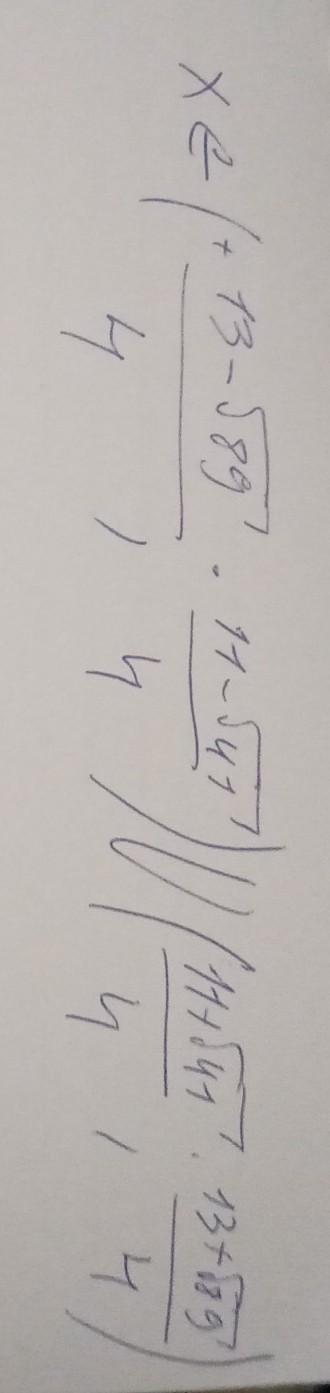
неравенства |f(x)| < g(x) решаются следующим образом
- g(x) < f(x) < g(x) или система f(x) < g(x) и f(x) > -g(x)
f(x) = x² - 6x + 5
g(x) = x/2
x² - 6x + 5 < x/2 (1)
x² - 6x + 5 > - x/2 (2)
1. f(x) < g(x)
x² - 6x + 5 < x/2
2x² - 12x + 10 - x < 0
2x² - 13x + 10 < 0
D = 13² - 4*2*10 = 169 - 80 = 89
x12 = (13 +- √89)/4
2(x - (13+√89)/4)(x - (13-√89)/4) < 0
применяем метод интервалов
+++++++++(13-√89)/4 ---------------- (13+√89)/4 +++++++
x ∈ ( (13-√89)/4 , (13+√89)/4)
примерно оценим числа (13-√89)/4 ≈ 0.892
(13 + √89)/4 ≈ 5.608
2. x² - 6x + 5 > -x/2
2x² - 12x + 10 + x > 0
2x² - 11x + 10 > 0
D = 11² - 4*2*10 = 121 - 80 = 41
x12 = (11 +- √41)/4
2(x - (11+√41)/4)(x - (11-√41)/4) > 0
применяем метод интервалов
+++++++++++++(11-√41)/4 ---------------- (11+√41)/4 ++++++++++++++
x ∈ ( -∞, (11-√41)/4) U ((11+√41)/4, +∞)
опять оценим (11-√41)/4 ≈ 1.149
(11+√41)/4 ≈ 4.351
получили
x ∈ ( (13-√89)/4 , (13+√89)/4)
x ∈ ( -∞, (11-√41)/4) U ((11+√41)/4, +∞)
++++++(13-√89)/4 ------------------------------------------ (13+√89)/4 +++++++
++++++++++++++++(11-√41)/4 ---------------- (11+√41)/4 ++++++++++++++
пересекаем и получаем
x ∈ ( (13-√89)/4, (11-√41)/4) U ((11+√41)/4 , (13+√89)/4)