Решить неравенство
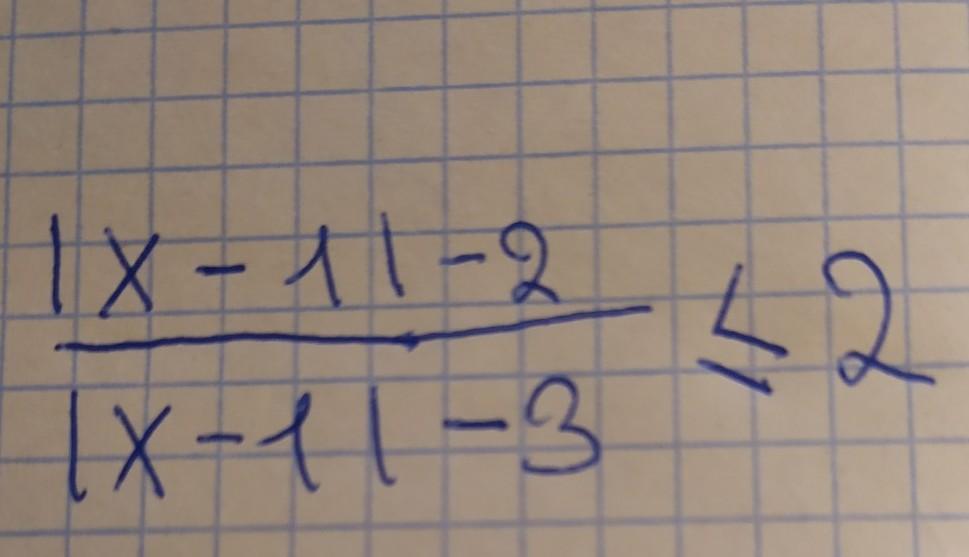
Ответы

( |x - 1| - 2)/(|x - 1| - 3) ≤ 2
ОДЗ |x-1| ≠ 3
x - 1 ≠ 3 ⇒ x ≠ 4
x - 1 ≠ -3 ⇒ x ≠ - 2
( |x - 1| - 2)/(|x - 1| - 3) - 2 ≤ 0
( |x - 1| - 2 - 2|x - 1| + 6)/(|x - 1| - 3) ≤ 0
(4 - |x - 1|)/(|x - 1| - 3) ≤ 0
раскрываем модуль
1. |x - 1| = x - 1 x ≥ 1
(4 - (x - 1))/((x - 1) - 3) ≤ 0
(5 - x)/(x - 4) ≤ 0
(x - 5)/(x - 4) ≥ 0
применяем метод интервалов
+++++++++(4) ---------------- [5] ++++++++++
x ∈ (-∞, 4) U [5, +∞)
вспоминаем ограничения
x ≥ 1 x ≠ 4
получили x ∈ [1, 4) U [5, +∞)
2. |x - 1| = -(x - 1) = 1 - x x < 1
(4 - (1 - x))/((1 - x) - 3) ≤ 0
(3 + x))/(-2 - x) ≤ 0
(3 + x))/(2 + x) ≥ 0
применяем метод интервалов
+++++++++[-3] ------------ (-2) +++++++++
x ∈ (-∞, -3] U (-2, +∞)
вспоминаем ограничения
x < 1 x ≠ -2
x ∈ (-∞, -3] U (-2, 1)
объединяем оба решения
x ∈ (-∞, -3] U (-2, 4) U [5, +∞)