Предмет: Алгебра,
автор: sergeydubov2002
Даю 20 баллов, 11 класс алгебра!!!
Приложения:
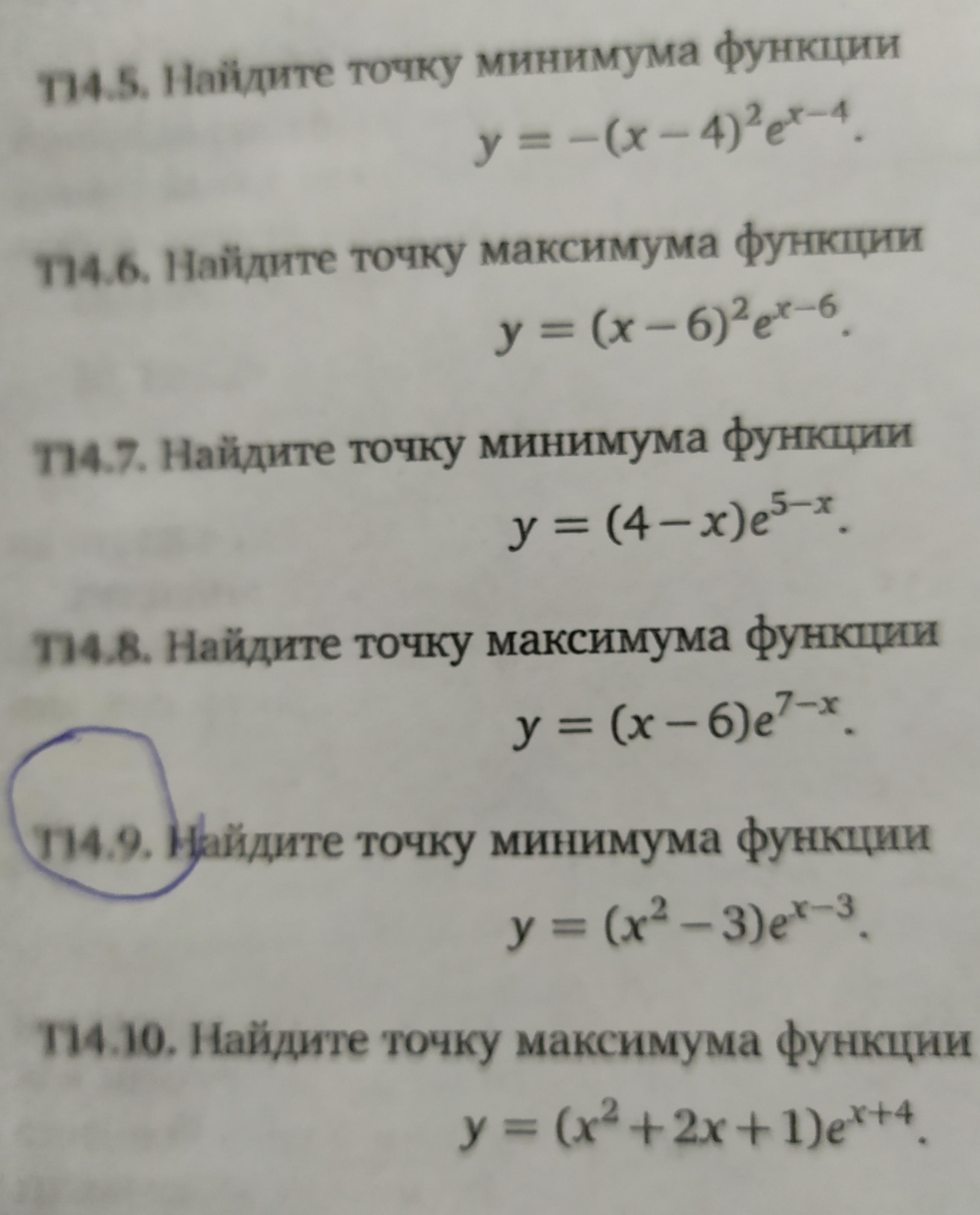
Ответы
Автор ответа:
0
Ответ:
Точка минимума
Объяснение:
Найдём производную:
Решим уравнение
На промежутке (-Infinity;1) функция убывает, а на промежутке (1;+Infinity) - возрастает, значит точка х=1 - точка минимума
Автор ответа:
0
Ответ:
найдем производную
у'=e^(x-3)(x^2-3)+e^(x-3)(2x)=e^(x-3)(x^2-3+2x)
найдем нули x^2+2x-3=0
x1=1 x2=-3
e^(x-3) всегда положительно
определим смену знака производной при переходе
через критические точки.
при переходе через 1 производная меняет знак с минуса
на плюс, и следовательно в этой точке имеется минимум.
y(1)=(1^2-3)e^(1-3)=-2/e^2
Похожие вопросы
Предмет: Другие предметы,
автор: Vem1x
Предмет: МХК,
автор: grebenukruslana9
Предмет: Химия,
автор: marina2473892
Предмет: История,
автор: toverLine
Предмет: Алгебра,
автор: Fugo1337