Предмет: Математика,
автор: tsibin228ru
Найдите значения a при котором корни уравнения: x^2 + (a+7)*x+a-4=0
Противоположные числа.
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Приложения:
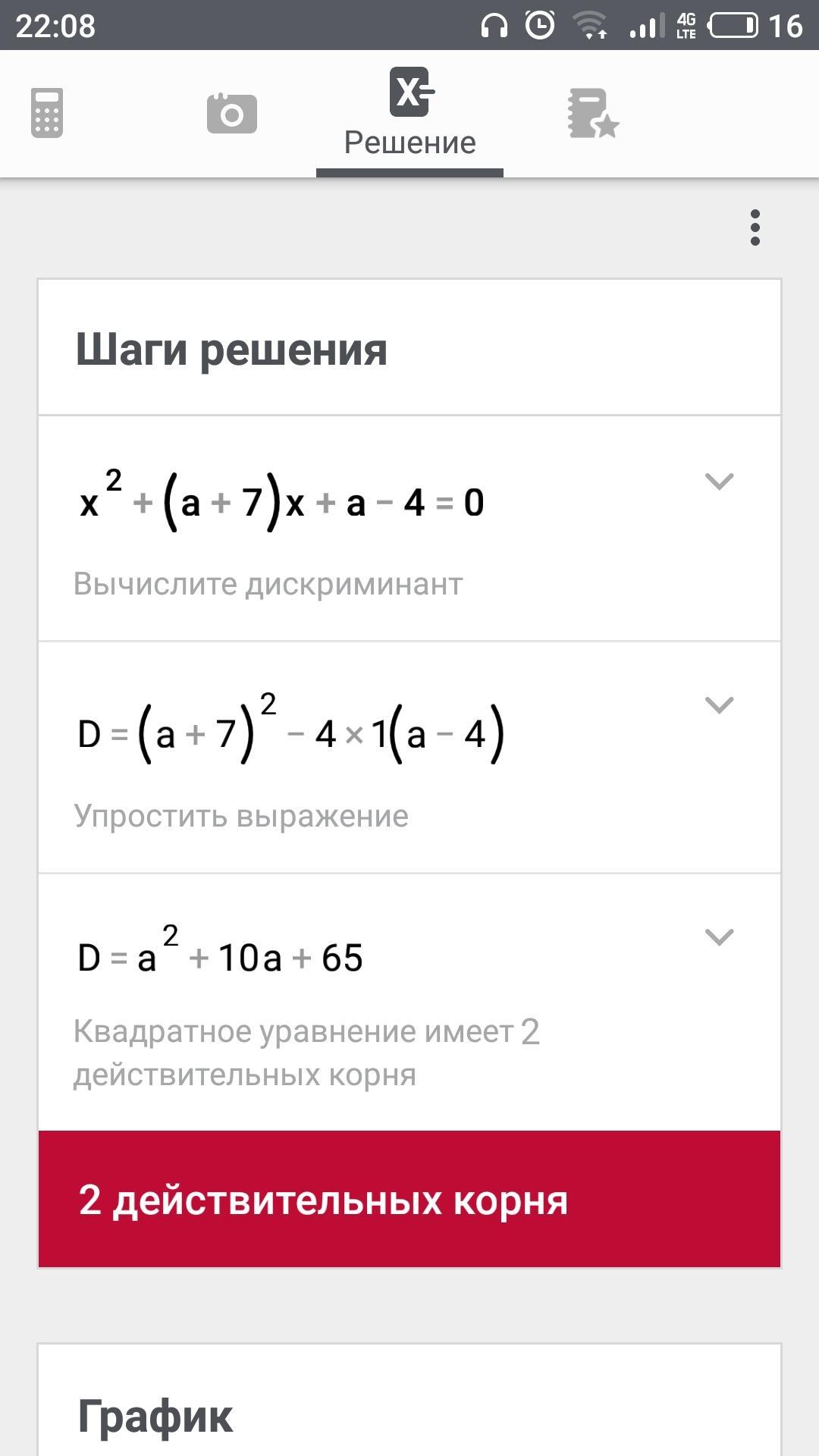
Автор ответа:
0
Ответ:
корни целые когда дискриминант может быть представлен в виде квадрата
найдем дискриминант получим
D=(16/(4-a)) + a^2
легко заметить что целые корни при целом a тогда когда целый дискриминант
чтобы дискриминант был целым необходимо |4-a|<16 и |4-a| был кратен 16
то есть -12 < a < 20
с этими условиями у нас только a=-12 a=-4 a=0 a=2 a=3 a=5 a=6 a=8 a=12 a=20
Дискриминант равен квадрату числа только при значениях 0 3 5
В этих случаях дискриминант равен 4 25 9 соответсвенно
Осталось проверить корни при этих значениях
(-a+-VD)/2
получаем
при
a=0 x1,2=+-1
a=3 x1=1 x2=-4
a=5 x1=-4 x2=-1
Ответ a=0 3 5
Пошаговое объяснение:
Похожие вопросы
Предмет: Литература,
автор: tumoniukanna
Предмет: Алгебра,
автор: vladislavdmitriev189
Предмет: Алгебра,
автор: messisuper447
Предмет: Литература,
автор: ксюшечка7523