Предмет: Математика,
автор: polarmedbed
Обчислить границу стремящуюся к нулю
Приложения:
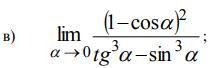
Ответы
Автор ответа:
1
Ответ:
в) +∞
Пошаговое объяснение:
в) Используем тригонометрические тождества
1)
2)
Похожие вопросы
Предмет: Українська література,
автор: Il12345
Предмет: Алгебра,
автор: dedushkamatematik
Предмет: Физика,
автор: FortunaYT
Предмет: Литература,
автор: ФёдороваАнна
Предмет: Математика,
автор: 228Supreme2281337