Предмет: Математика,
автор: sasha6980
Всем привет , если не трудно помогите пожалуйста кому не трудно, заранее спасибо .
Приложения:

Ответы
Автор ответа:
1
Ответ:
Ответы объяснении
Пошаговое объяснение:
Приложения:
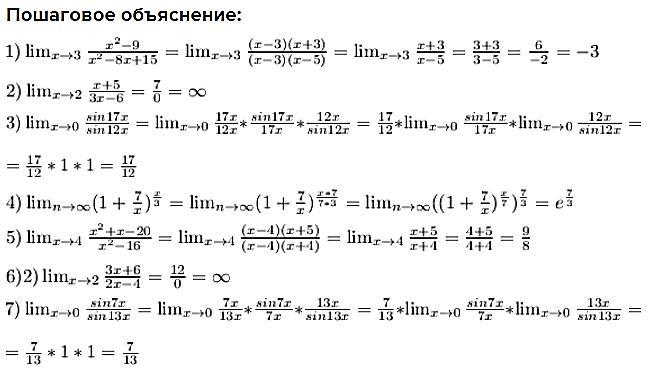
sasha6980:
У меня даже полностью не просматривается
Сейчас как рисунок добавлю
Всё с решением
Хорошо спасибо
Удачи
Я хочу предложить тебе подзаработать нужно решить задания
Как на это смотришь
Извини, по заказу не работаю
Ну а так решишь за баллы ?
Я решаю интересные мне задачи, а в заказе не всегда интересные задачи
Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: mihajlovalkovec
Предмет: Українська мова,
автор: anastasiavixx
Предмет: Математика,
автор: elmera6767
Предмет: Химия,
автор: papakarla228