Предмет: Алгебра,
автор: SofiaSkM
Здравствуйте, помогите решить
Приложения:
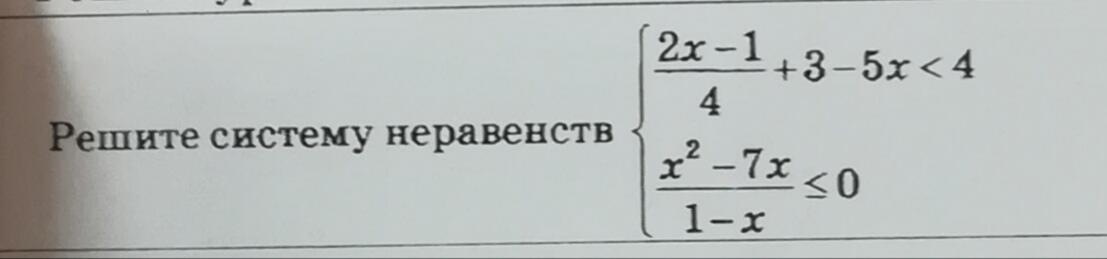
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Алгебра,
автор: vihopensofijka
Предмет: Другие предметы,
автор: torobekovakanykey
Предмет: Геометрия,
автор: bebrochka999
Предмет: Музыка,
автор: vladikon2005
Предмет: Литература,
автор: mrtke