Question

Помогите с монотонностью функций Пожалуйстаааа

Answer 1

Ответ:

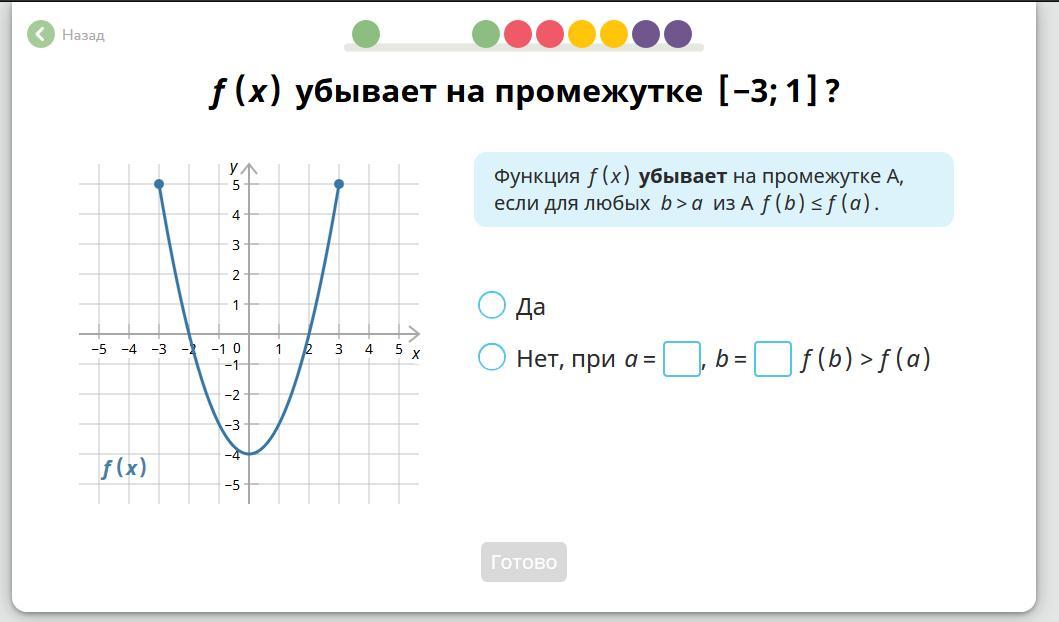
"Нет, при b = 1, a = 0 (b > a) f(b) > f(a)".

Пошаговое объяснение:

Утверждение о том, что функция убывает на [-3;1], ошибочно. Нажимаем кнопку "НЕТ", докажем это:

Выберем два значения а и b из этого промежутка. Например, а = 0 и b = 1.

0 < 1, т.е. а < b. Если бы функция была убывающей на этом отрезке, то f(a) > f(b). Но у нас это не так:

f(a) = f(0) = - 4;

f(b) = f(1) = - 3;

- 4 < - 3, т.е. f(a) < f(b).

Получили противоречие определению, даём ответ:

"Нет, при b = 1, a = 0 (b > a) f(b) > f(a)".