Предмет: Алгебра,
автор: nastysh20011
Помогите с интегралами!!! Пожалуйста!! Ничего не понимаю( Объясните что и как. Пожалуйссстааа
Приложения:
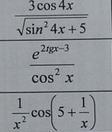
Ответы
Автор ответа:
1
nastysh20011:
Спасибо вам огромное!! Ничего в них не понимаю, но я пытаюсь разобраться) Вы мне очень помогаете) Спасибо!
Похожие вопросы
Предмет: Математика,
автор: lasemomi1793
Предмет: Математика,
автор: Winchester9347
Предмет: Математика,
автор: klassikw6922
Предмет: История,
автор: Анжеліка121
Предмет: Математика,
автор: Ажырдынгынбош