Предмет: Алгебра,
автор: Mikhail68
Найти x в уравнении 3^(3x)+3^(2x+1)=3^x+3
Приложения:
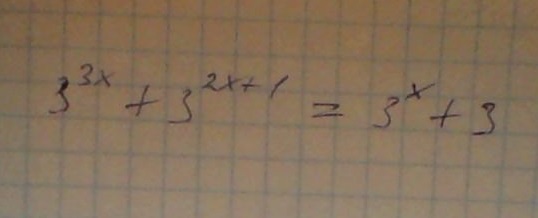
Ответы
Автор ответа:
0
3^(3x)+3*3^2x-3^x-3=0
3^x=t
t^3+3t^2-t-3=0
t^2(t+3)-(t+3)=0
(t+3)(t^2-1)=0
t>0
t=1
3^x=1
x=0
3^x=t
t^3+3t^2-t-3=0
t^2(t+3)-(t+3)=0
(t+3)(t^2-1)=0
t>0
t=1
3^x=1
x=0
Похожие вопросы
Предмет: Физика,
автор: arystanovaayym
Предмет: Информатика,
автор: SanekSmir
Предмет: Алгебра,
автор: IceeSword
Предмет: Математика,
автор: Аноним