Question

Доказать теоремы
1. в равнобедренном треугольнике медиана проведённая к основанию является биссектрисой и высотой
2. в равнобедренном треугольнике высота проведённая к основанию является медианой и биссектрисой

Answer 1

Высота. медиана, биссектриса в равнобедренном треугольнике
Доказательство теоремы номер 2:

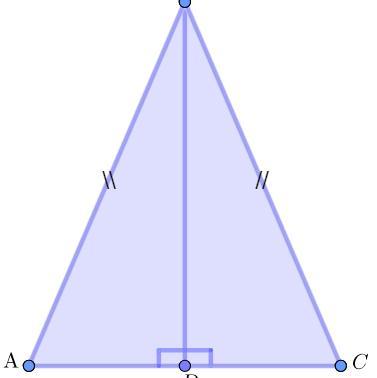
Дан Δ ABC.
Из точки В проведем высоту BD.
Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
Прямые АС и BD называются перпендикуляром.
В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
АВ = ВС — боковые стороны равны.
Стороны АD = СD, т.к. точка D отрезок делит пополам.
Следовательно Δ ABD = ΔBCD.
Биссектриса, высота и медиана это один отрезок - BD