Предмет: Математика,
автор: sukkas
Помогите решить интегралы. 9 и 10 пример. N=21
Приложения:
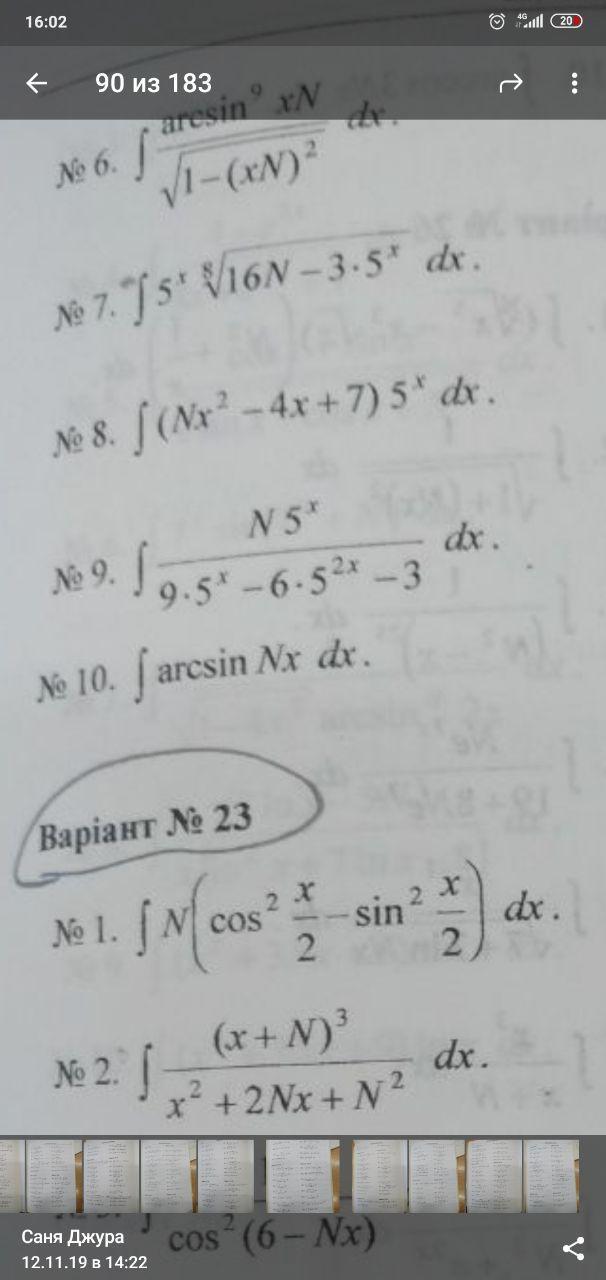
Ответы
Автор ответа:
0
Автор ответа:
0
Ответ во вложении Пошаговое объяснение:
Приложения:

xx2yyuuygg82:
пожалуйста помоги мне с математикой
Похожие вопросы
Предмет: Математика,
автор: kkatjka
Предмет: Химия,
автор: yzenikent
Предмет: Математика,
автор: daniellabogina
Предмет: Математика,
автор: SvetlanaAstanovka
Предмет: Литература,
автор: vikyssssik