Предмет: Математика,
автор: abdulovasofi
Помогите вычислить интеграл
Приложения:

Аноним:
Формулу понижения степени используйте
Ответы
Автор ответа:
2
Решение на фотографии
Приложения:
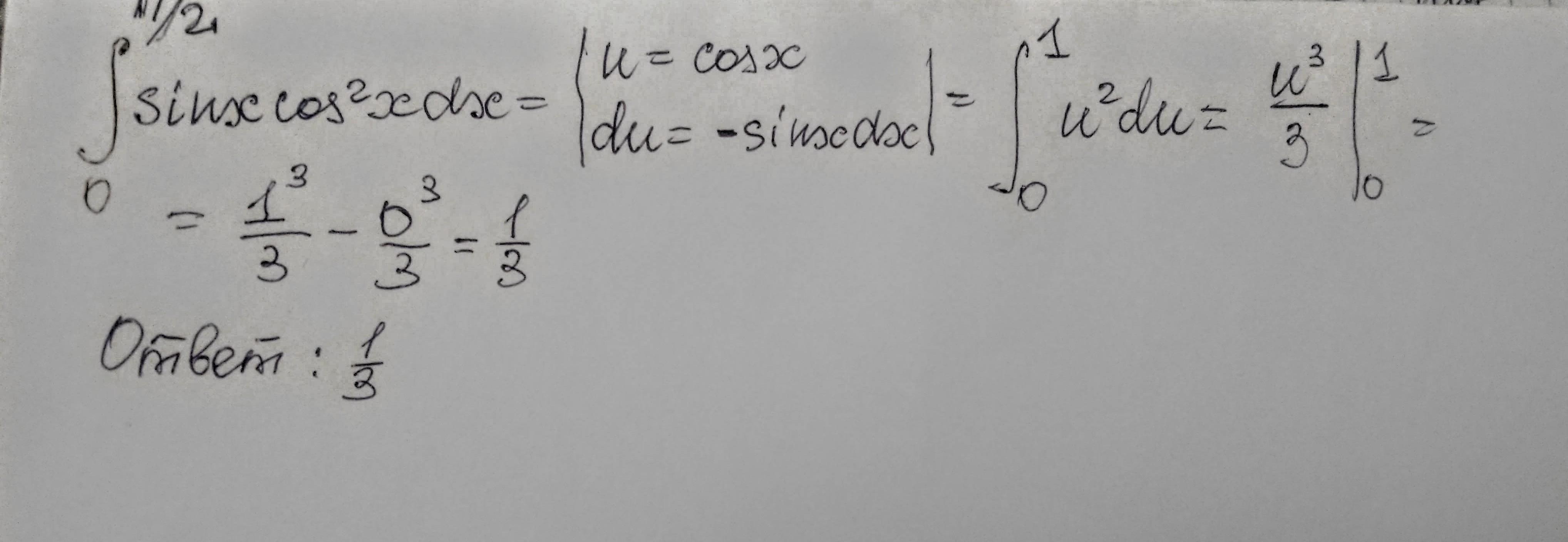
Если делаете замену, то и меняются пределы интегрирования
там где появилось u, пределы от 1 до нуля. и ответ тот же. Две последние строчки напрасны.
да, уже поняла... невнимательность(( но исправить не успела, к сожалению
исправите позже. Модератор пришлет на исправление.
Автор ответа:
2
Похожие вопросы
Предмет: Русский язык,
автор: namazovfirengiz
Предмет: Физика,
автор: Ziganhinanika
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: papa33
Предмет: Алгебра,
автор: Аноним