Question

Найти угол между векторами а{7;1} и в{5;5
даю 30 б

Answer 1

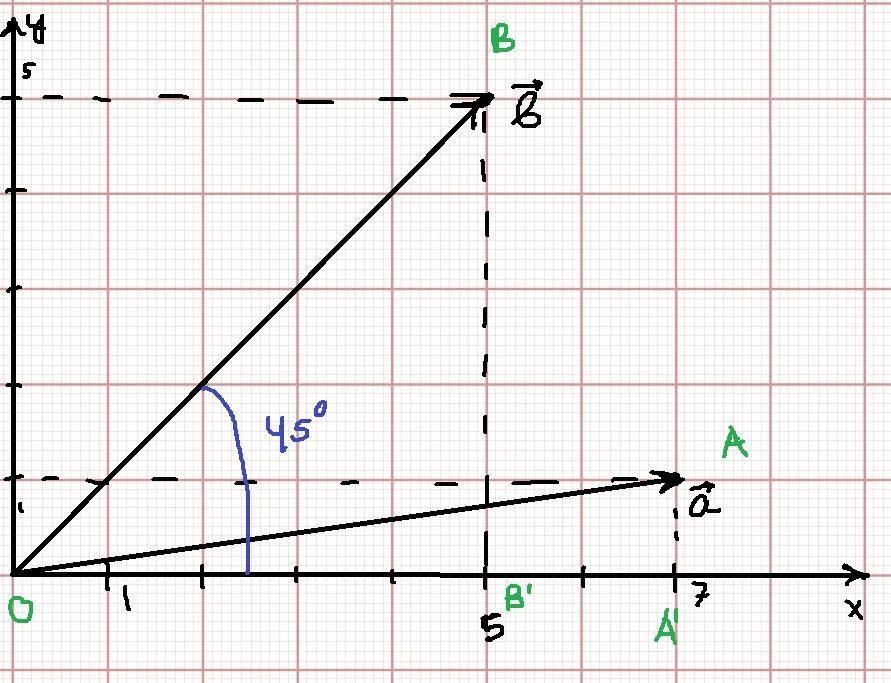
Я построил эти векторы. Не нужно быть учёным, чтобы понять, что угол между вектором b и осью x равен 45 градусам. Хотя бы потому, что катеты прямоугольного треугольника OBB' равны.

Найдём длину вектора a по формуле:

l = √(x^2 + y^2)

l = √(AA'^2 + AO'^2)

l = √(1^2 + 7^2) = √(1 + 49) = √50 = 5√2

Найдём острый угол AOA'

Для начала найдём его синус:

sin(∠AOA') = AA'/OA = 1/(5√2) = √2/10

Найдём угол через обратную функцию

∠AOA' = arcsin(√2/10)

Тогда угол между векторами будем равен

45 - arcsin(√2/10)

arcsin(√2/10) - не табличное значение. Самая точная формулировка так и останется выглядеть. Но если хочется посчитать примерно, то я округлил значение arcsin(√2/10)

45 - arcsin(√2/10) ≈ 45 - 8,13 = 36,87°