Предмет: Математика,
автор: hop688
помогите решить задачу
Приложения:
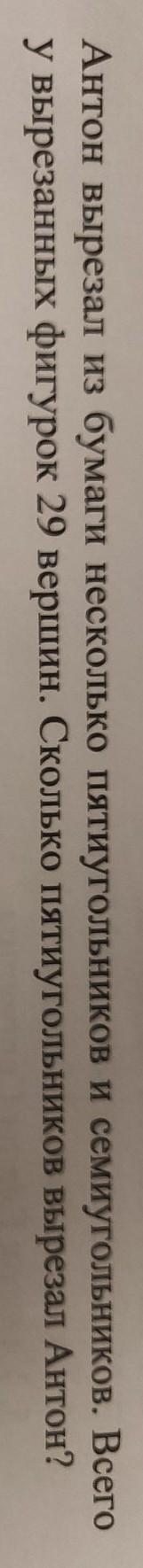
Ответы
Автор ответа:
1
Предположим, что семиугольник только один. Тогда количество вершин у пятиугольников равно 29 − 7 = 22. Этого не может быть, потому что число 22 на 5 не делится.
Если семиугольников два, то количество вершин у пятиугольников равно 29 − 14 = 15. Значит, может быть три пятиугольника.
Если семиугольников три, то количество вершин у пятиугольников равно 29 − 21 = 8, чего быть не может.
Больше трёх семиугольников быть не может.
или
7 + 7 + 5 + 5 + 5 = 29
2 • 7 + 3 • 5 = 29
Похожие вопросы
Предмет: История,
автор: Vilenapro2010
Предмет: Немецкий язык,
автор: Stas1234556
Предмет: Математика,
автор: student125682
Предмет: Математика,
автор: Наталья1718
Предмет: Математика,
автор: RoYanovich