Предмет: Математика,
автор: Okkrr
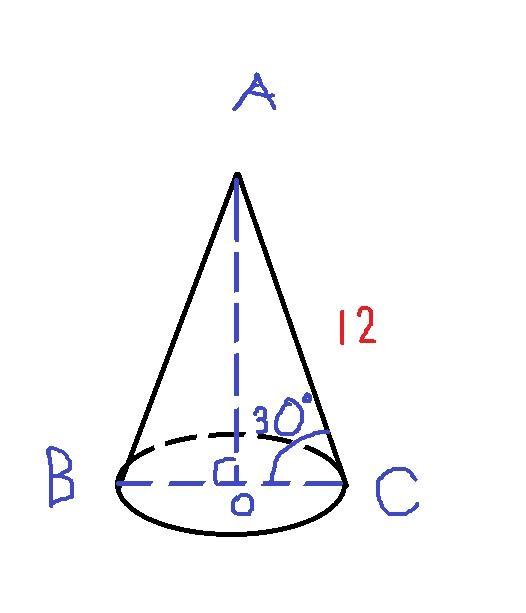
Образующая конуса равна 12 см наклонена к плоскости основания под углом 30 найти площадь осевого сечения, площадь боковой поверхности и объём конуса.
Ответы
Автор ответа:
1
Для начала построим сечение, перпендикулярное основанию плоскости, как я показал на рисунке. Если мы опустим высоту AO, то получим два прямоугольных треугольника. Рассмотрим, например, AOC. Против угла 30 градусов лежит катет, равный половине гипотенузы. Значит, высота AO = AC/2 = 12/2 = 6 см. Найдём OC по теореме Пифагора:
√(AC^2 - AO^2) = √(12^2 - 6^2) = 6√3
В свою очередь OC является радиусом круга, который лежит в основании конуса. Найдём его площадь по формуле:
S = πR^2
S = π * (6√3)^2 = 36 * 3π = 108π ≈ 339,292 см^2
Найдём объём конуса по формуле
V = 1/3 Sh
V = 1/3 * 108π * 6 = 2 * 108π = 216π ≈ 678,584 см^3
Найдём площадь боковой поверхности по формуле:
S = πRl, где l - длина образующей
S = 12 * 6√3π = 72√3 * π ≈ 391,781 см^2
Приложения:
Похожие вопросы
Предмет: Математика,
автор: PLZdaiOTVET554
Предмет: Физика,
автор: Banderlog8641
Предмет: Алгебра,
автор: varooooolll
Предмет: История,
автор: Kanieva01
Предмет: История,
автор: Аноним