Предмет: Алгебра,
автор: Аноним
Решение квадратных корней
Приложения:
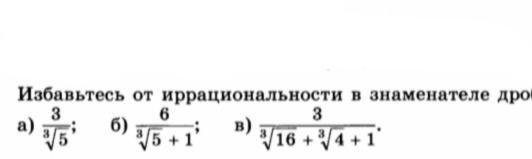
25102003p7qtjs:
Что нужно?
на фото
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: eowlsif
Предмет: Литература,
автор: selickaakira35
Предмет: Математика,
автор: taisiapolackovaa
Предмет: Алгебра,
автор: donkikeev