Предмет: Алгебра,
автор: lankina3652
Какую наименьшую площадь может иметь прямоугольный треугольник,
катеты которого лежат на координатных осях, а гипотенуза является отрезком
касательной к графику функции f (x) = 2x²-6 ?
Vilmar:
ответа нет? у меня получилось 8 целых и 5/16
Ответы
Автор ответа:
0
Ответ: 9
Объяснение:
Если катеты лежат на осях, то координаты вершин А (0;у) и В (х;0)
Приложения:
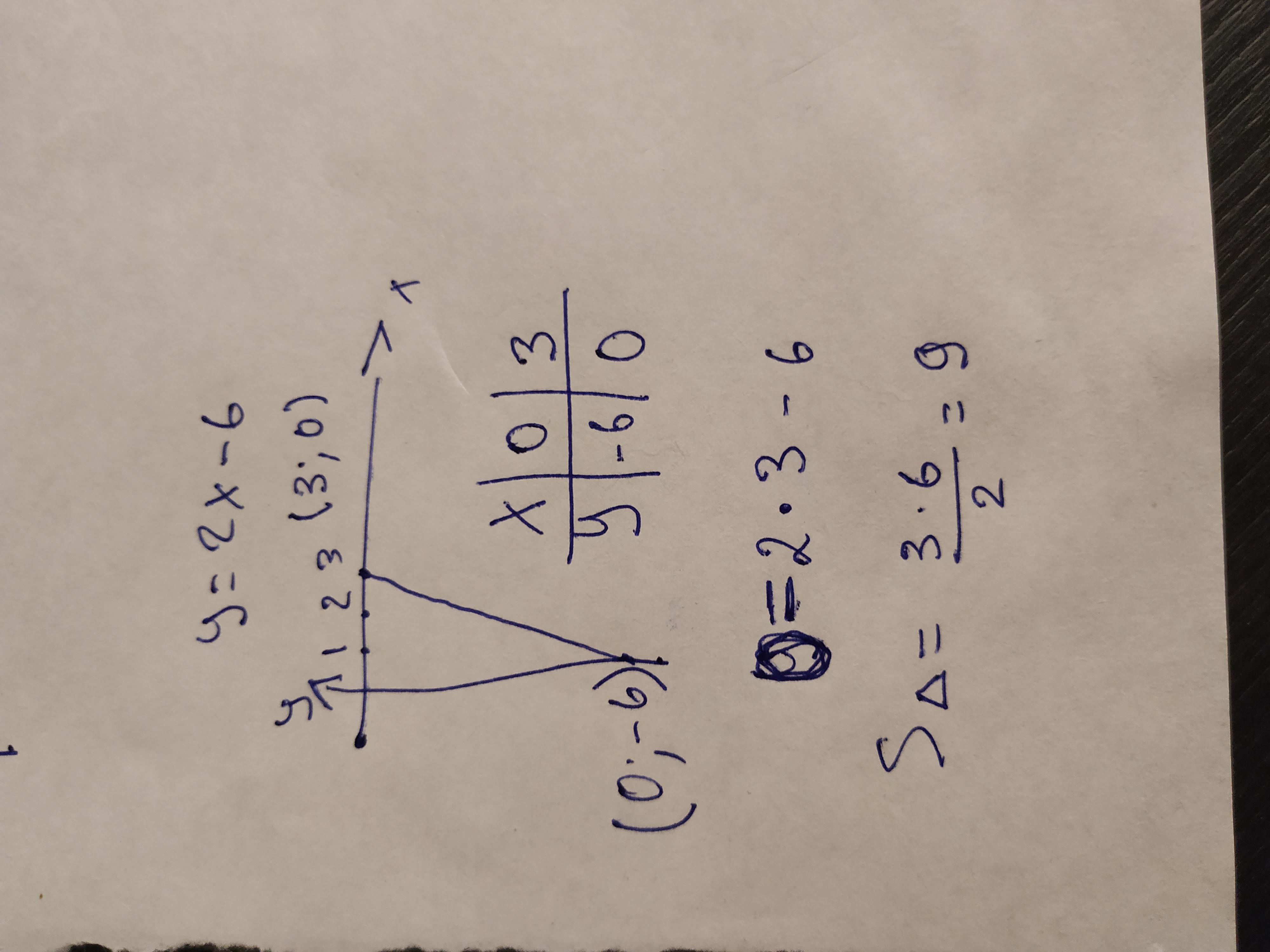
куда ты х квадрат дел?
Автор ответа:
0
Ответ: 8,46 см²
Объяснение: y=2x²-6 парабола с вершиной в точке(0;-6) и корнями (2;-2)
проведем прямую через точки (2;0) и (0;-6)
-2y=-6x+12
y=3x-6
теперь найдем уравнение касательной к параболе
2x²-6=3x-n (тк у параболы и касательной одна общая точка , то дискриминант будет равен 0)
2x²-3x-6+n=0
D=0⇒b²-4ac=0
9-4*(n-6)*2=0
9+48-8n=0
8n=57
n=57/8⇒ уравнение касательной
у=3x-57/8 она пересекает ось OX в точке
3x-57/8=0
3x=57/8
x=19/8
ось OY пересекает в точке
y=-57/8
тогда наименьшая площадь прямоугольного треугольника ограниченного осями OX и OY и касательной к параболе y=2x²-6
S=(x*y)/2=(19/8*57/8)/2=1083/128=8.46 см²
Похожие вопросы
Предмет: Английский язык,
автор: timur09136
Предмет: Литература,
автор: dimadmitruk131
Предмет: Математика,
автор: antriada
Предмет: Алгебра,
автор: vikavikalalala