Question

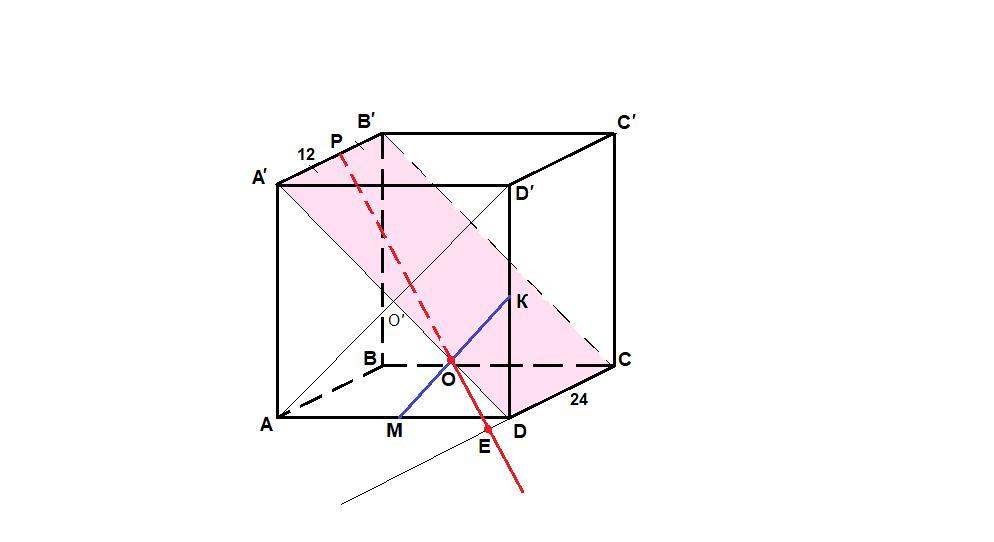
Из середины ребра A′B′ куба ABCDA′B′C′D′ провели прямую, которая пересекает прямую CD в некоторой точке E, а также пересекает прямую, проходящую через середины ребер AD и DD′. Найдите длину отрезка DE, если сторона куба равна 24.

Answer 1

Ответ:

4

Объяснение:

Р - середина ребра А'В'.

Пересекающиеся прямые РЕ и CD задают плоскость, которая пересекает основание ABCD по прямой CD.

Параллельные плоскости пересекаются секущей плоскостью по параллельным прямым.

(А'В'С')║(АВС), значит линия пересечения (РСЕ) и (А'В'С'), проходящая через точку Р, должна быть параллельна CD. Это ребро A'В'.

Итак, плоскость (РСЕ) пересекает грань AA'D'D по прямой A'D.

М и К - середины ребер AD и DD'. Прямая МК пересекает A'D в точке О. И только в этой точке прямая РЕ может пересечь прямую МК.

МК - средняя линия треугольника AD'D, значит О делит пополам O'D, тогда OD = 1/4 A'D.

ΔA'PO ` ΔDEO по двум углам (∠PA'O = ∠EDO = 90°, углы при вершине О равны, как вертикальные), тогда

$\dfrac{DE}{A'P}=\dfrac{OD}{OA'}$

$\dfrac{DE}{12}=\dfrac{1}{3}$

DE = 12/3 = 4