Предмет: Математика,
автор: zemishaguseynova80
при каком значении m уравнение x^2+(2m-3)x+m-2=0 имеет единственный корень. Пожалуйста помогите срочно!!!
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Уравнение x²+(2m-3)x+m-2=0 имеет один корень, если его дискриминант D = b²-4ac = 0.
В нашем уравнении a=1, b=2m-3, c=m-2.
D = b²-4ac = (2m-3)²-4(m-2)=4m²-12m+9-4m+8=4m²-16m+17=0.
Решая квадратное уравнение 4m²-16m+17=0, получаем,
что его дискриминант = (-16)²-4*4*17=256 - 272 = -16<0, действительных корней нет.
Ответ: ни при каких значениях m.
Автор ответа:
4
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
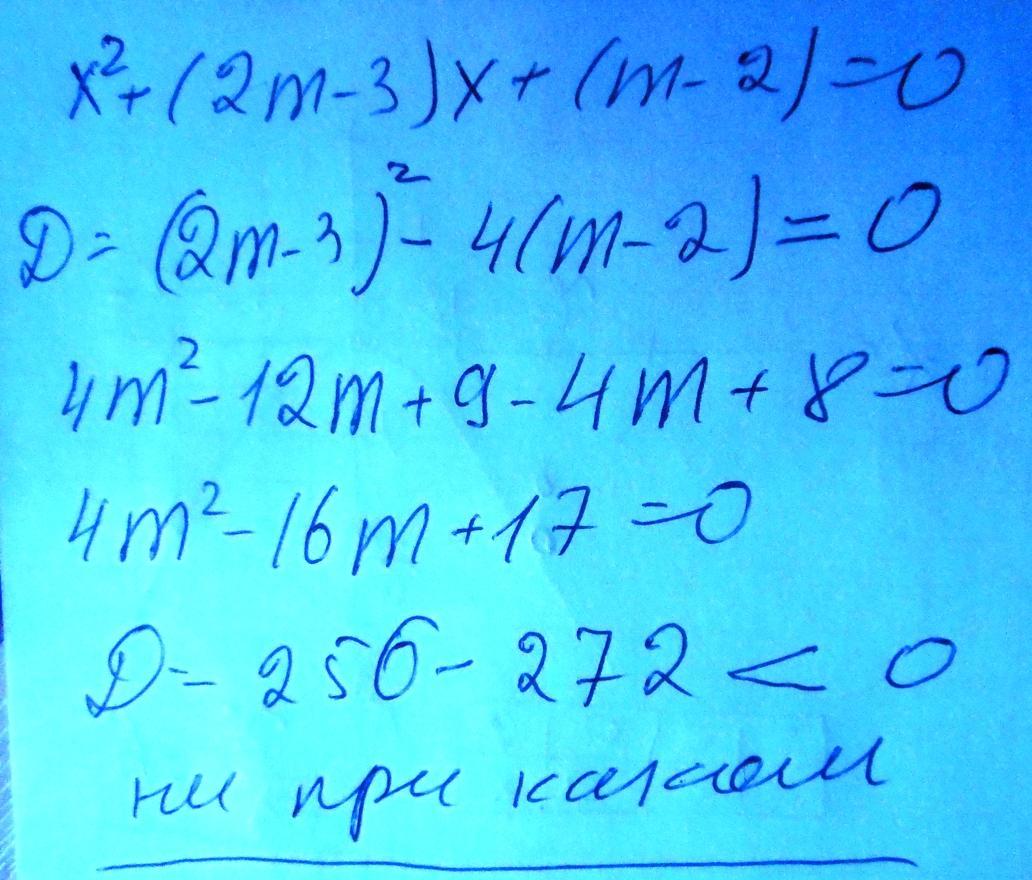
Похожие вопросы
Предмет: Английский язык,
автор: sxegege1
Предмет: Математика,
автор: timofijstasuk
Предмет: Алгебра,
автор: amirovaamirovameilru
Предмет: Математика,
автор: len84
Предмет: Математика,
автор: arisa1