Предмет: Алгебра,
автор: RainbowChickeen
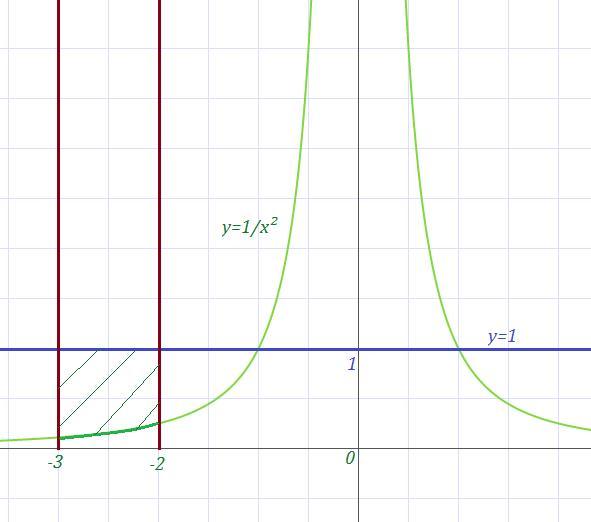
Найдите площадь фигуры ограниченной линиям:

Ответы
Автор ответа:
0
Ответ: .
Объяснение:
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: losha987654321
Предмет: Математика,
автор: serdtfyiuk6561
Предмет: Математика,
автор: MultiFrost2129
Предмет: Математика,
автор: Tiashi