Question

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC Расстояние от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найти площадь параллелограмма ABCD.

Answer 1

Сделаем построения и введём обозначения, как показано на рисунке. Пусть O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём

Отрезки и OK равны как радиусы вписанной в треугольник ABC окружности, то есть Рассмотрим треугольники ALO и AOK, они прямоугольные, углы LAO и OAK равны, AO — общая, следовательно, треугольники равны, откуда Аналогично из равенства треугольников COM и COK получаем а из равенства треугольников BOL и BOM — Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:



Площадь параллелограмма равна произведению высоты на основание:

Рассмотрим треугольники ABC и ACD, AB равно CD, AD равно BC, углы ABC и ADC равны, следовательно, треугольники ABC и ACD равны. Поэтому площадь треугольника ABC равна половине площади параллелограмма:

Площадь параллелограмма равна:

Ответ:

Answer 2

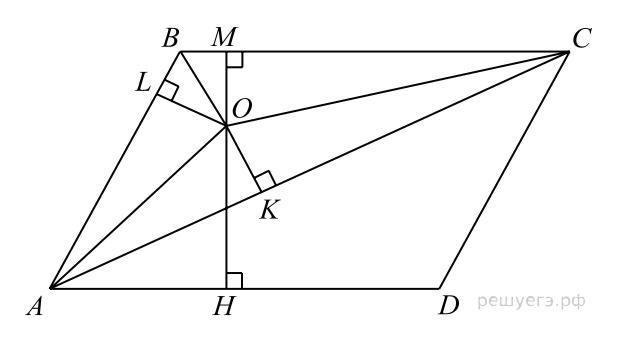
Насколько мне помнится, то тут нужно решать объяснениями, если да то: Пусть O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём

Отрезки и OK равны как радиусы вписанной в треугольник ABC окружности, то есть Рассмотрим треугольники ALO и AOK, они прямоугольные, углы LAO и OAK равны, AO — общая, следовательно, треугольники равны, откуда Аналогично из равенства треугольников COM и COK получаем а из равенства треугольников BOL и BOM — Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:

Площадь параллелограмма равна произведению высоты на основание:

Рассмотрим треугольники ABC и ACD, AB равно CD, AD равно BC, углы ABC и ADC равны, следовательно, треугольники ABC и ACD равны. Поэтому площадь треугольника ABC равна половине площади параллелограмма т.е 168