Предмет: Математика,
автор: ManOfTheFuture
Исследовать функцию методом дифференциального исчисления. Можно побыстрее, пожалуйста.
Приложения:
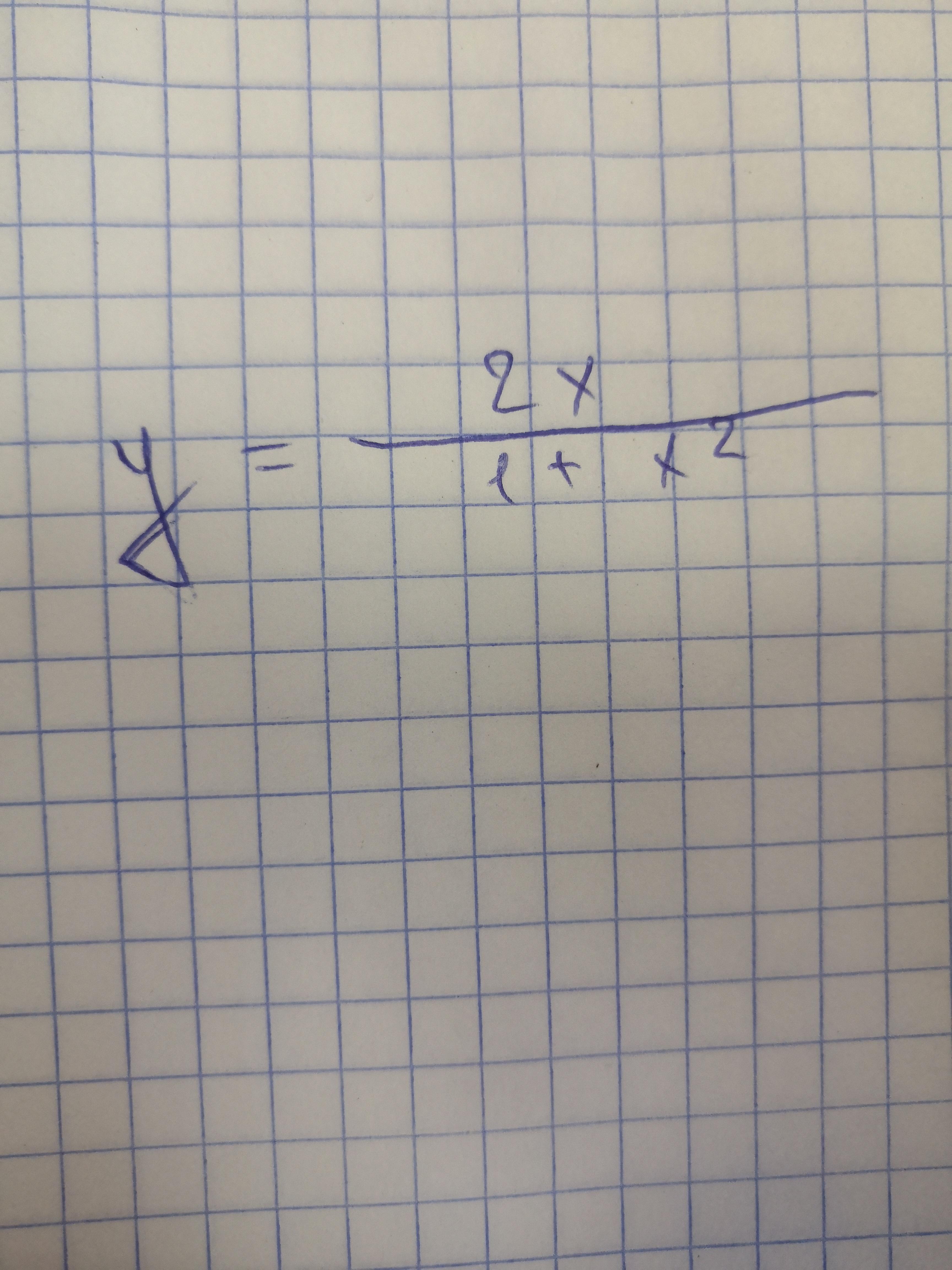
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
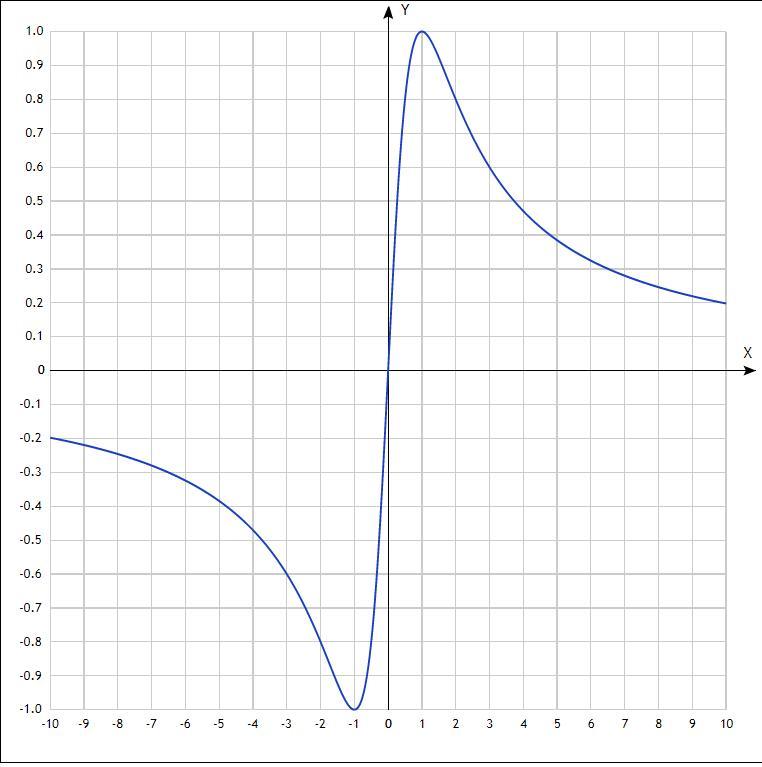
1) область определения функции: x ∈ R
2) проверим на четность:
y(-x) = -2x/(1 + x²) = -y(x) - функция нечетная
3) функция не периодическая
4) y = 0 только при х = 0, значит, точка пересечения с осями только (0; 0)
5) функция непрерывна
6) y' = (2(1 + x²) - 4x²)/(1+x²)² = (2 - 2x²)/(1 + x²)² = 0
2 - 2x² = 0
2x² = 2
x = -1 или x = 1
y'' = (4x³ - 12x)/(1+x²)³
y''(-1) > 0
y''(1) < 0
x = -1 - точка минимума
x = 1 - точка максимума
7) находим асимптоты:
x = 0 - асимптота
найдем наклонные асимптоты:
больше нет асимптот
Приложения:
Похожие вопросы
Предмет: Литература,
автор: AsinastraSenpai
Предмет: Математика,
автор: kriterpro
Предмет: Алгебра,
автор: SyrexFF
Предмет: Математика,
автор: kovalanna78