Предмет: Алгебра,
автор: mainecoon88605
Найдите производную функции, помогите пожалуйста.
Приложения:
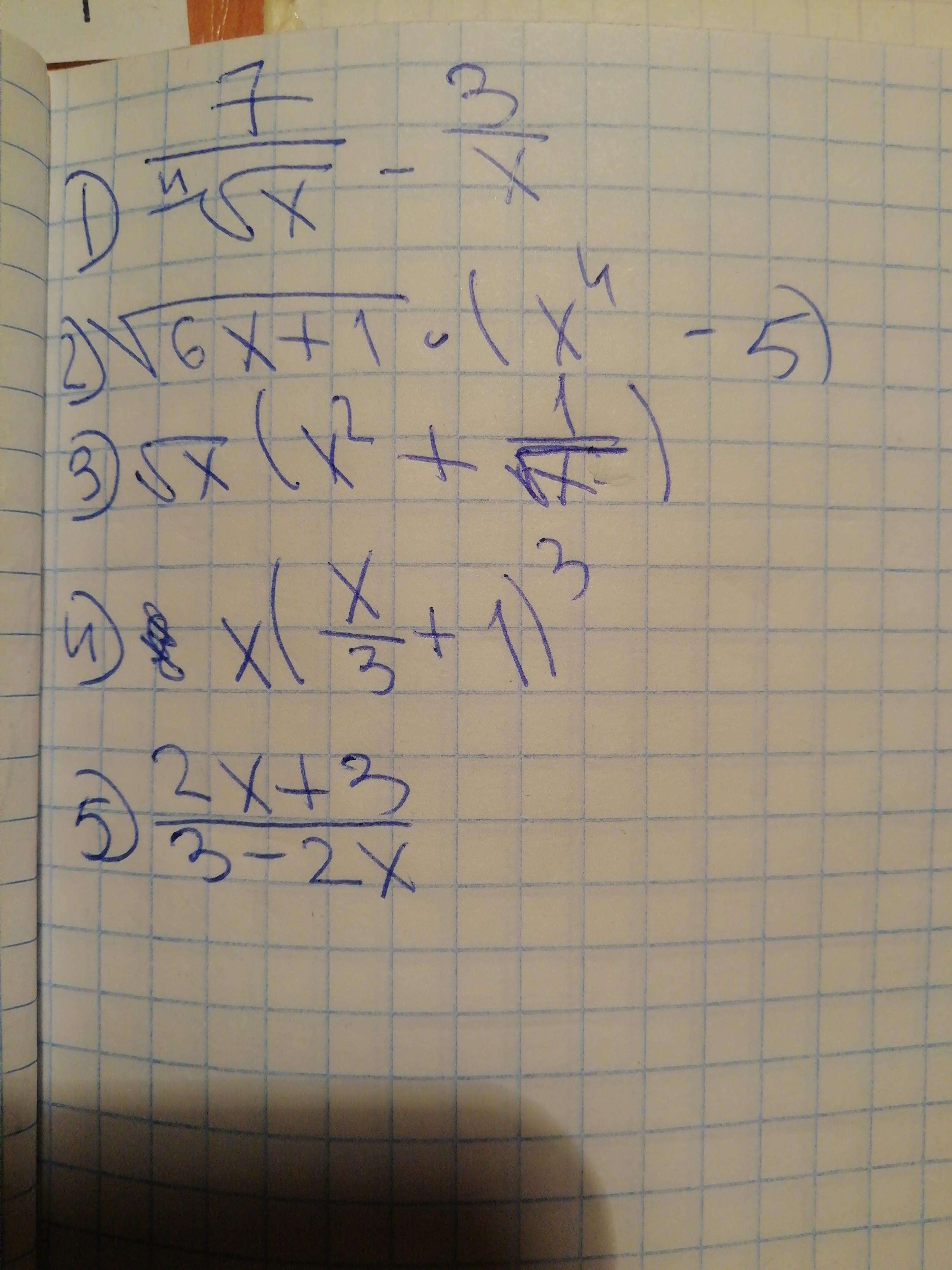
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: pupil05g31
Предмет: Геометрия,
автор: dsfgh43
Предмет: Алгебра,
автор: yura2217
Предмет: Литература,
автор: 65564515456
Предмет: География,
автор: sova753