Question

земля мне пухом а, может кто-то помочь?

Answer 1

Ответ:

$x^{2} +(y-(-\frac{27}{6} ))^{2}=(\frac{45}{6} )^{2}$

Пошаговое объяснение:

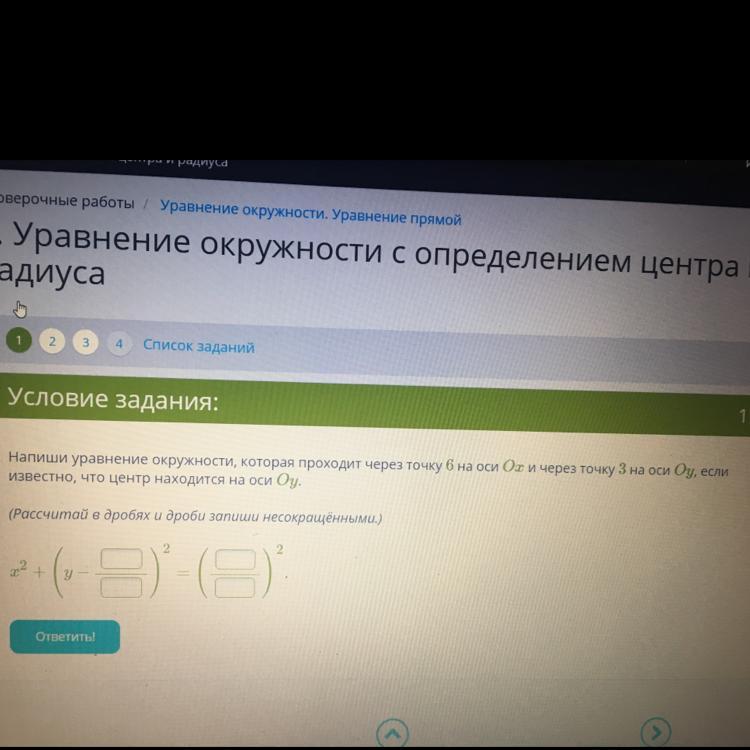
Так как центр окружности находится на оси Оу, то центр находится в точке с координатами О(0; у0). По условию окружность проходит через точку 6 на Ох, то есть через точку плоскости с координатами А(6; 0), и через точку 3 на Оу, то есть через точку плоскости с координатами В(0; 3).

По определению, все точки окружности находятся от центра в равном расстоянии, равной радиусу R. Находим для заданных точек А и В это расстояние:

$|OA|=\sqrt{(0-6)^{2} +(y0-0)^{2} }=\sqrt{36+y0^{2} }$

$|OB|=\sqrt{(0-0)^{2} +(y0-3)^{2}} = \sqrt{(y0-3)^{2}}$

Так как эти расстоянии равны радиусу, то они равны и :

$R^{2}=|OA|^{2}=|OB|^{2}$ или

36+y0² = (y0-3)² или 36+y0² = y0²-6·у0+9 или 6·у0= -27. Отсюда у0=-27/6 (по условию задачи дроби не сократим!).

Значит, центр окружности находится в точке (0; -27/6). Тогда радиус окружности равен:

R=|OB|=|y0-3|=| -27/6-3|= 27/6+18/6=45/6 (по условию задачи дроби не сократим!).

Ответ: $x^{2} +(y-(-\frac{27}{6} ))^{2}=(\frac{45}{6} )^{2}$