Предмет: Математика,
автор: niskofly
Решить задание с параметром
Приложения:
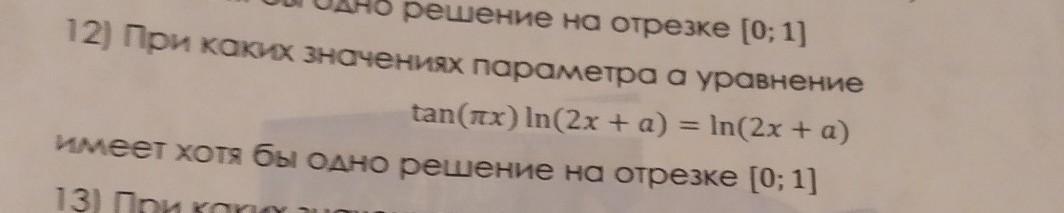
Simba2017:
я решила, но не могу ручаться за правильность ответа...
Ответы
Автор ответа:
1
(tg(πx)-1)ln(2x+a)=0
ОДЗ
2x+a>0; a>-2x
πx≠π/2+πk; x≠1/2+k (k⊂Z)
учитывая интервал по х: x≠0.5 ( при x=0.5 a=0)
1)ln(2x+a)=0; 2x+a=e^0=1; a=1-2x; x=0; a=1; x=1; a=-1
a=[-1;1]
2)tg(πx)=1
πx=π/4+πk
x=1/4+k (k⊂Z)
учитывая интервал по х: x=1/4-ответ от параметра не зависит. Главное чтобы при этом существовал ln(2x+a)-или другими словами 2x+a>0. Подставляя в него х=1/4, получу
2*1/4+a>0; a>-1/2.
То есть корень по тангенсу при =-1.4 существует при а>-1/2
Объединяя оба ответа по а=[-1;1]U(1/2;+∞) , получим общий ответ: Данное уравнение имеет хотя бы один корень на интервале x=[0;1] при a≥-1
Похожие вопросы
Предмет: Математика,
автор: lezginnr
Предмет: Химия,
автор: rodion228102rus
Предмет: Математика,
автор: abdurauftura
Предмет: Математика,
автор: vieronikalukin