Предмет: Математика,
автор: Andreykas1234567890
Очень срочно решение, даю максимум баллов!!!
Приложения:
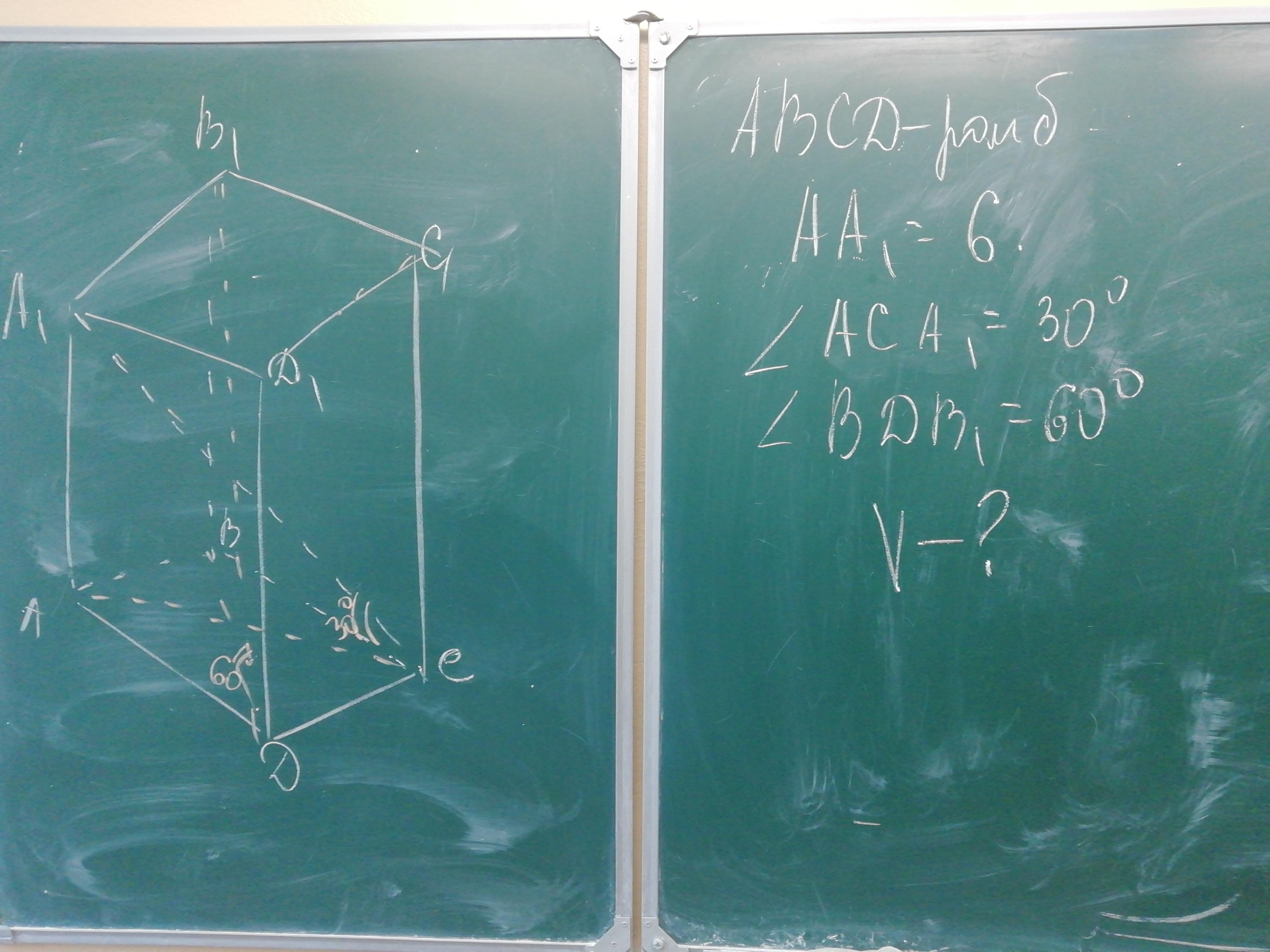
Andreykas1234567890:
Ну пж можно побыстрее
Ответы
Автор ответа:
1
досчитай намана,
я сейчас исправлю
Окей
я еще ошибку нашел сейчас доиспраалю
исправлю*
Напишешь когда уже точно конечный ответ будет
Это уже всё?
сейчас все, но у меня есь сомнение на правильность решения моего
есть*
Ага, по формуле V=S основания*h... А у тебя S основания почему то в квадрате
Похожие вопросы
Предмет: Физика,
автор: arsen5486
Предмет: Литература,
автор: zizylya
Предмет: Алгебра,
автор: sticher4889
Предмет: Физика,
автор: корн144