Предмет: Математика,
автор: Бодя2212
Вычислить частные производные функций
Обчислити частиннi похiднi функцiй
Приложения:
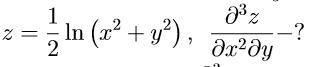
Ответы
Автор ответа:
1
Пошаговое объяснение:
Бодя2212:
https://znanija.com/task/33459413 хелп
Похожие вопросы
Предмет: Алгебра,
автор: Yuliya4208
Предмет: Алгебра,
автор: karinaasanova5303
Предмет: Математика,
автор: PlotnikovaY7900
Предмет: Биология,
автор: Saboneeva