Предмет: Алгебра,
автор: run4yourlife
Маленькая задача на векторы, помогите пожалуйста.
Приложения:
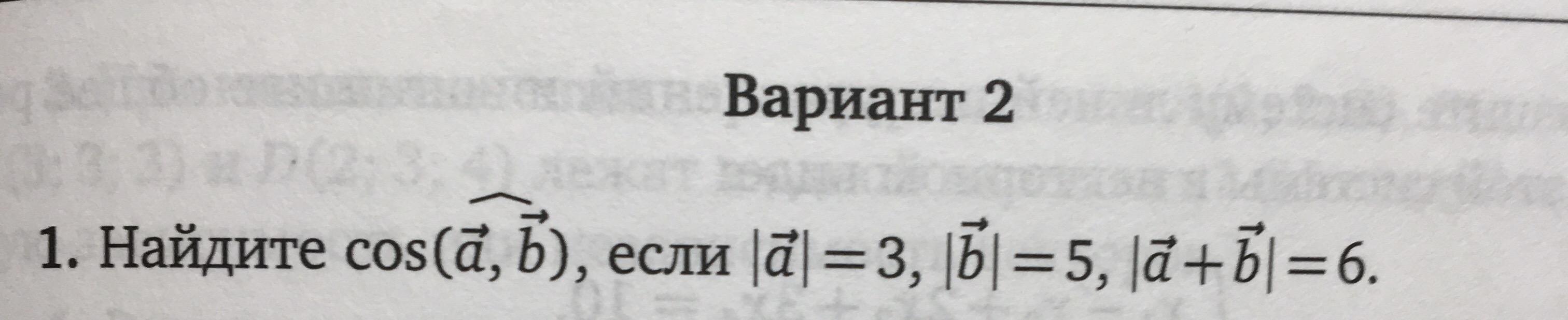
Ответы
Автор ответа:
1
Задача. Найдите косинус угла между векторами a и b, если |a| = 3, |b| = 5, |a+b| = 6
Решение:
В равенстве возводим обе части до квадрата
Косинус угла между векторами a и b :
Похожие вопросы
Предмет: Химия,
автор: lapkovania778
Предмет: Английский язык,
автор: emaksim504
Предмет: Русский язык,
автор: nnayapperssic
Предмет: Биология,
автор: Лапа2015