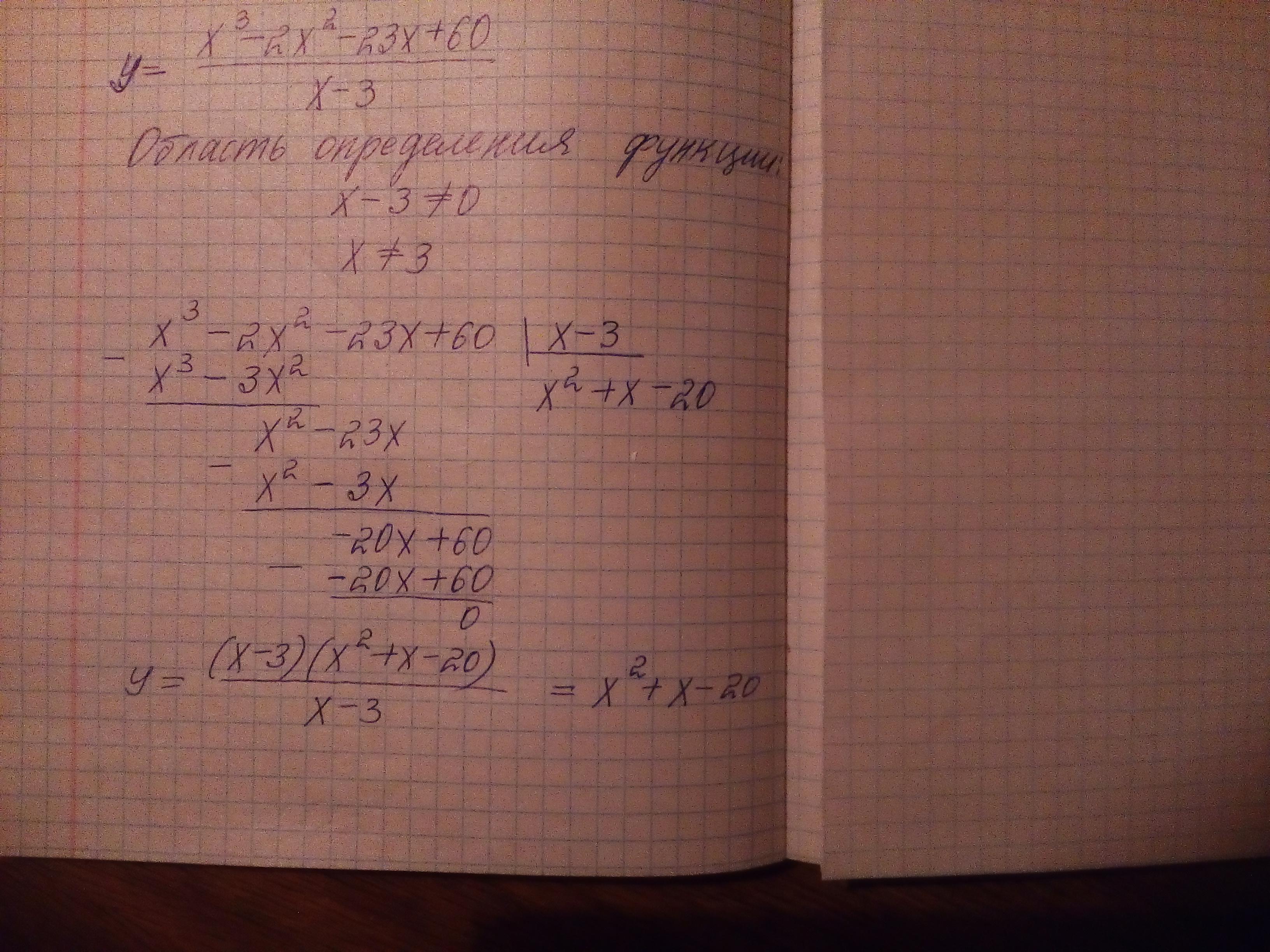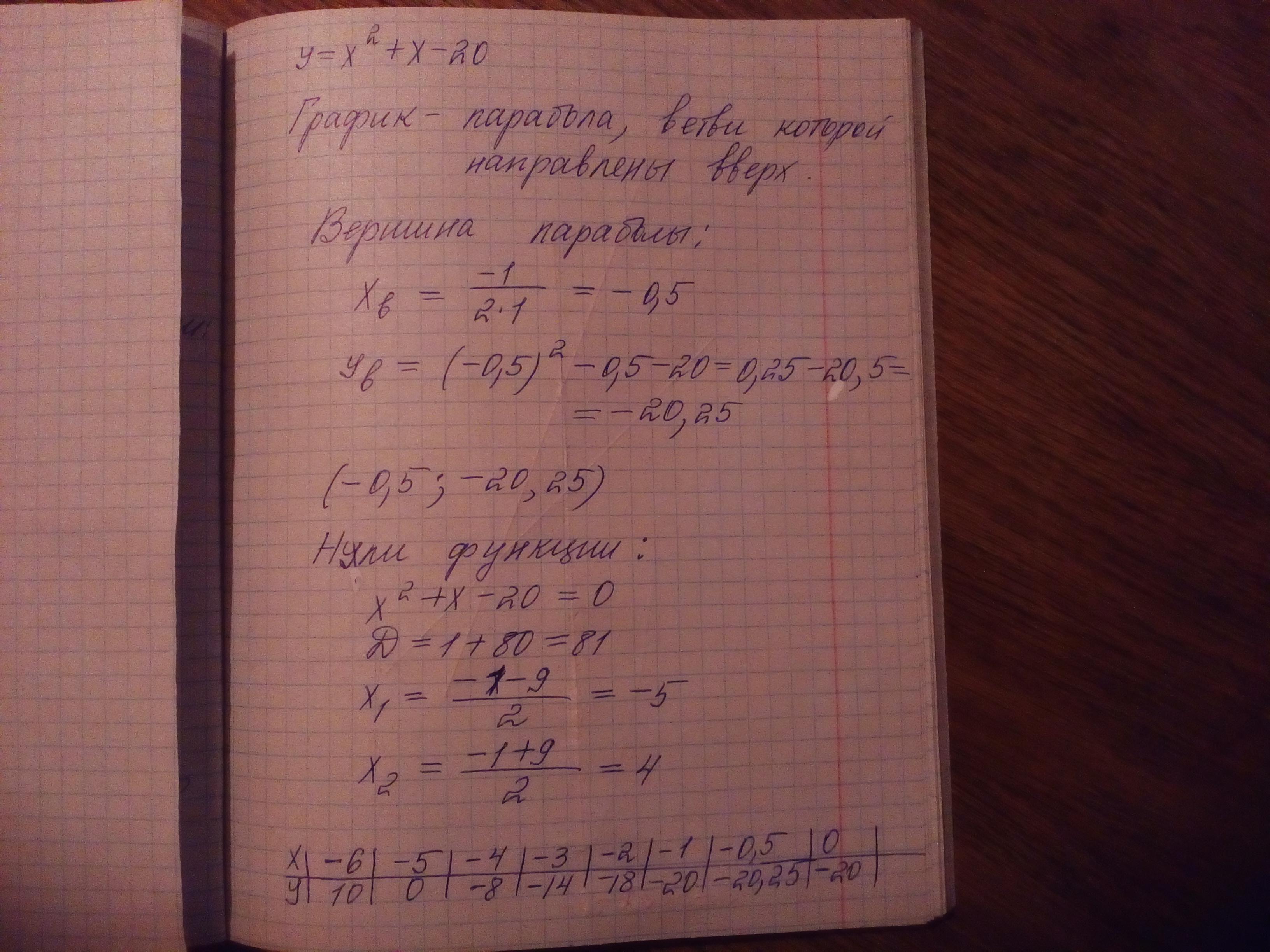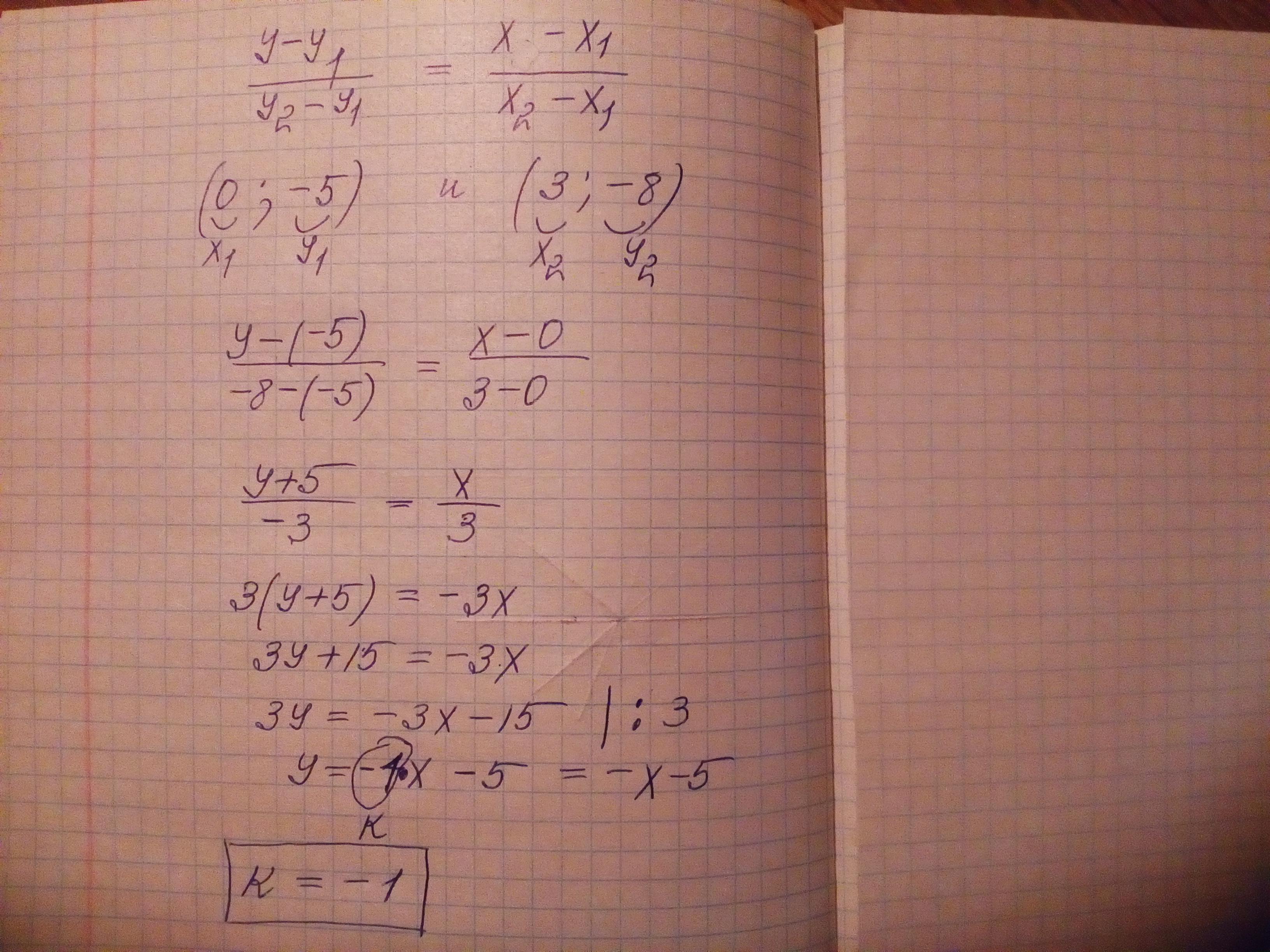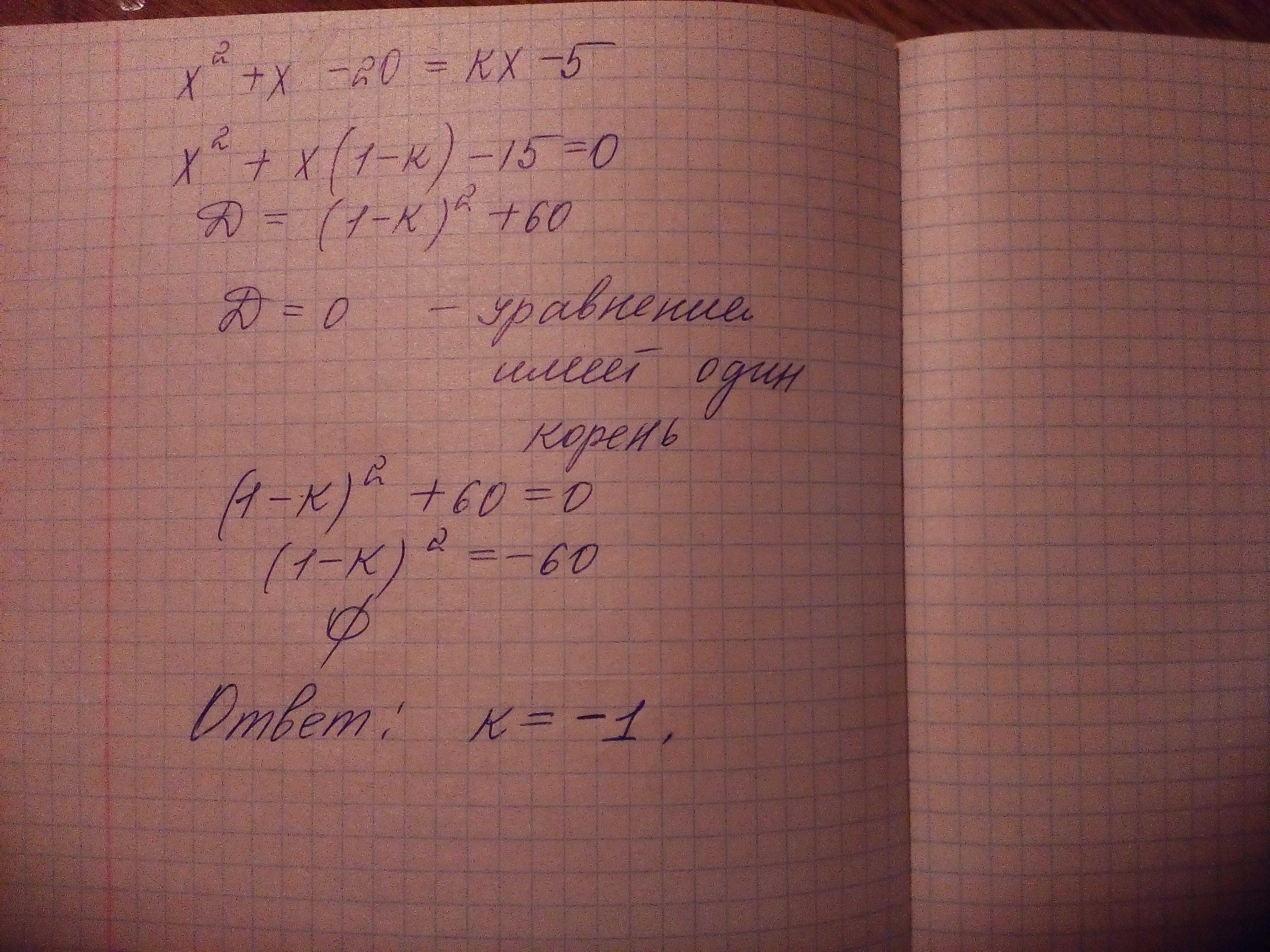Условие и вопрос на рисунке!!!
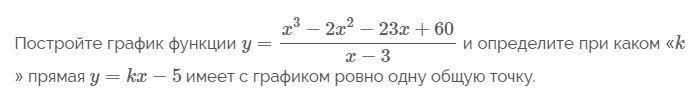
Ответы
Ответ:
нет решения
Объяснение:
Упростим первую функцию, поделив числитель на знаменатель. Получим y=x²+x-20.
Получим точку пересечения обеих функций, приравняв обе функции:
x²+x-20 = kx-5
x²+x(1-k)-15 = 0
Т.к. одна точка пересечения, то дискриминант будет равен нулю:
D= (1-k)²+60 = 0 => k²-2k+61=0
В последнем уравнении дискриминант <0, что говорит о том, что ровно одной общей точки между параболой и прямой нету.
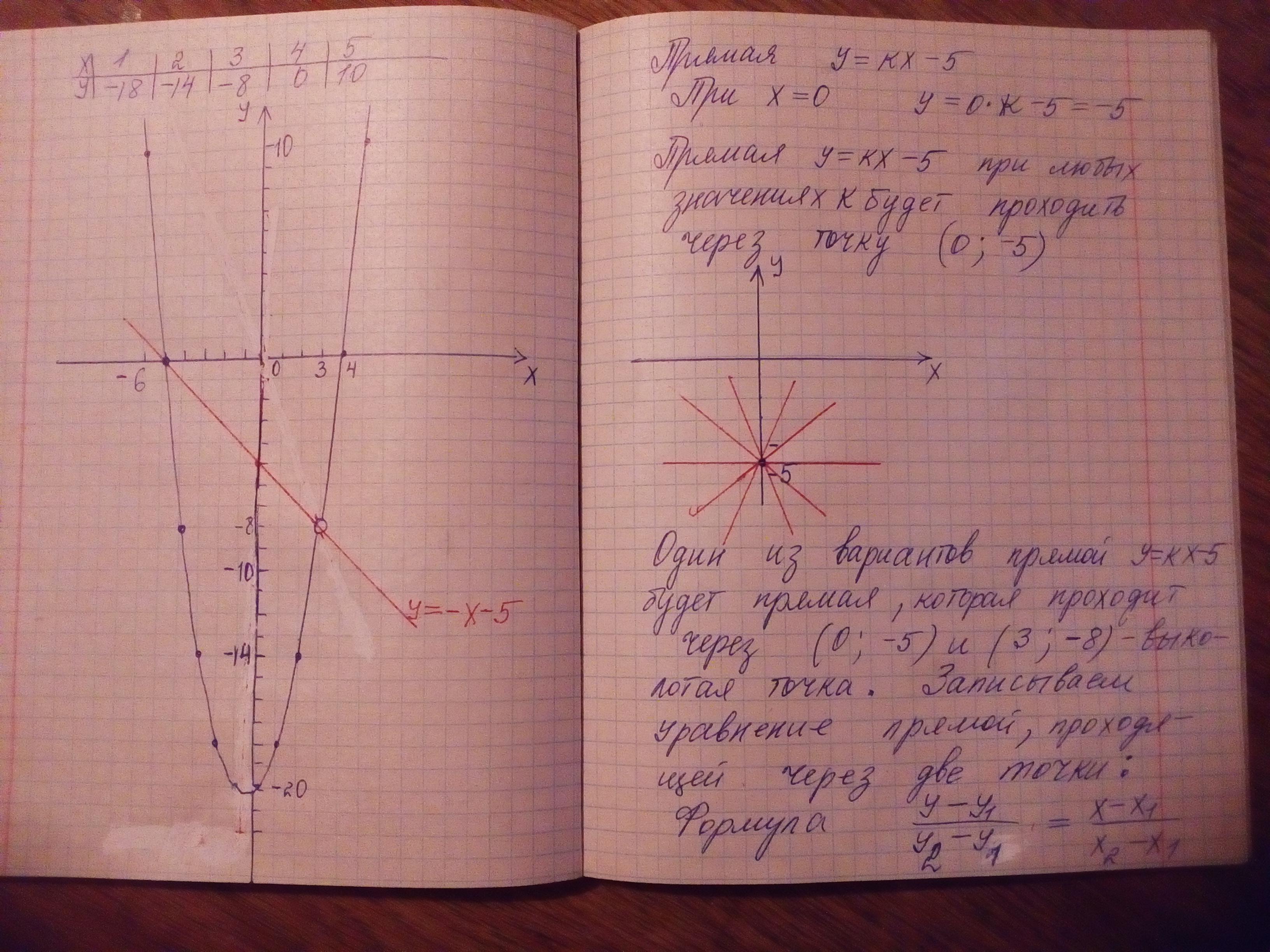
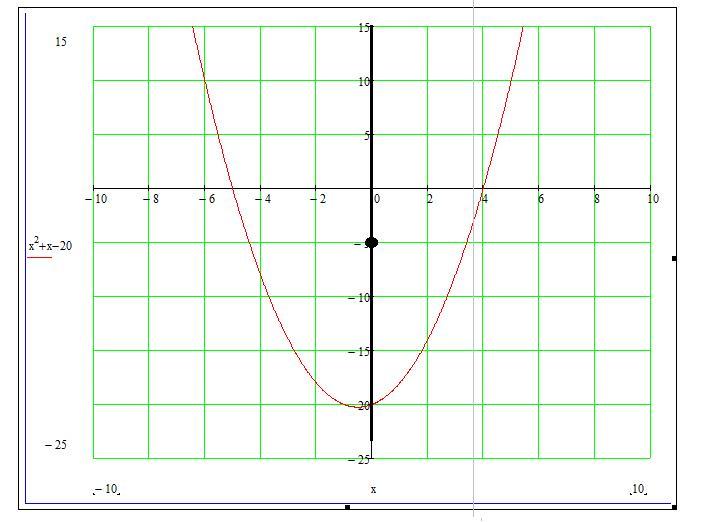
Можно поспорить с тем, что при k=±∞ будет одна единственная общая точка (см. рисунок). В действительности, прямая не будет идеально вертикальная, поэтому где-то вверху она ещё раз пересечёт параболу.
Чтобы это доказать, решим уравнение x²+x(1-k)-15 = 0. Получим две точки:
x1 = ( k-1 + √(k²-2k+61) ) / 2
x2 = ( k-1 - √(k²-2k+61) ) / 2
Подставим, например, в оба уравнения k=+∞
Получим:
x1 = ∞
x2 = 0
Как видим, прямая ещё раз пересечёт параболу на бесконечности. Тоже самое будет и при k=-∞
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!