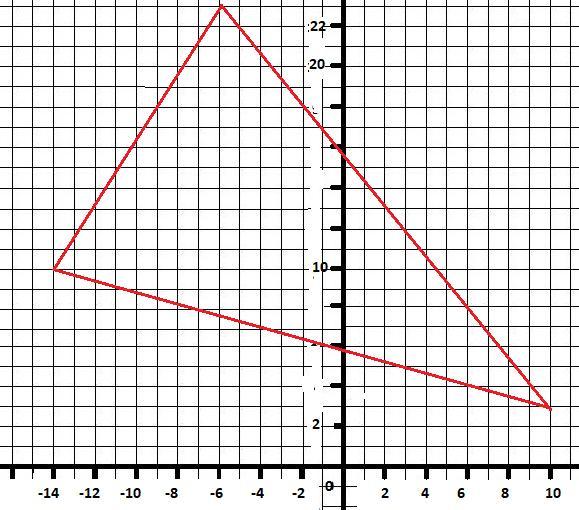
6. Даны координаты вершин треугольника ABC. Найти: 1) длину стороны BC; 2) уравнение линии BC; 3) уравнение высоты, проведенной из точки A; 4) величину угла B; 5) систему неравенств, определяющую треугольник ABC. Сделать чертеж.
A (-14,10), B (10,3), С (-8,27)
Ответы
РЕШЕНИЕ.
1) Длина стороны по теореме Пифагора.
ВС² = (Bx-Cx)²+(By-Cy)²=18²+(-24)²=324+576=900
BC = √900 = 30 - длина ВС - ответ.
2) Уравнение ВС.
ДАНО: В(10;3), С(-8;27) , НАЙТИ: Y = k*x + b
1) k = ΔY/ΔX = (Вy-Сy)/(Вx-Сx)=(3-(27))/(10-(-8))= - 4/3 (-1,33) - коэффициент наклона прямой
2) b=Вy-k*Вx=3-(- 4/3)*10= 16 1/3- сдвиг по оси ОУ
Уравнение Y(ВС) = - 4/3*x+16 1/3 - ответ
3) Уравнение высоты из А к ВС.
Высота AF перпендикулярна к ВС.
Коэффициент наклона по формуле:
K = -1/k = - 1/(-4/3) = 3/4 - наклон.
Теперь проводим прямую из точки А по заданному наклону.
Дано: Точка A(-14,10), наклон k = 0,75
b = Aу - k*Ax = 10 - (0,75)*(-14) = 20,5
Уравнение прямой - Y(A) = 0,75*x + 20,5 - высота AF - ответ.
4) Величина угла В между прямыми ВА и ВС.
Находим уравнение стороны АВ.
ДАНО: В(10;3), А(-14;10) . НАЙТИ: Y = k*x + b
1) k = ΔY/ΔX = (Вy-Аy)/(Вx-Аx)=(3-(10))/(10-(-14))= -7/24 - коэффициент наклона прямой
2) b=Вy-k*Вx=3-(- 7/24)*10= 5 11/12- сдвиг по оси ОУ
Уравнение Y(ВА) = - 7/24*x+ 5 11/12 - сторона ВА.
tgβ = (k₂ - k₁)/(1 + k₁k₂) =(-7/24 - (-4/3))/(1 7/18) = 25/24 : 25/18 = 3/4
β = arctg(3/4) = 0.644 рад = 36,87° - угол В - ответ.
5)Система неравенств описания АВС.
Нужно третье уравнение - стороны АС
ДАНО: С(-8;27), А(-14;10) . НАЙТИ: Y = k*x + b
1) k = ΔY/ΔX = (Сy-Аy)/(Сx-Аx)=(27-(10))/(-8-(-14))= 2 5/6 - коэффициент наклона прямой
2) b=Сy-k*Сx=27-(2 5/6)*(-8) = 49 2/3 - сдвиг по оси ОУ
Уравнение Y(СА) = 2 5/6*x + 49 2/3 - сторона АС.
Составляем систему уравнений из трех уравнений прямых.
1) у + 4/3*x = -16 1/3
2) у +7/24*x = 5 11/12
3) у - 2 5/6*x = 49 2/3
Чертеж с рисунком задачи в приложении.