Предмет: Математика,
автор: DEADpoll
Найти область сходимости ряда
Приложения:
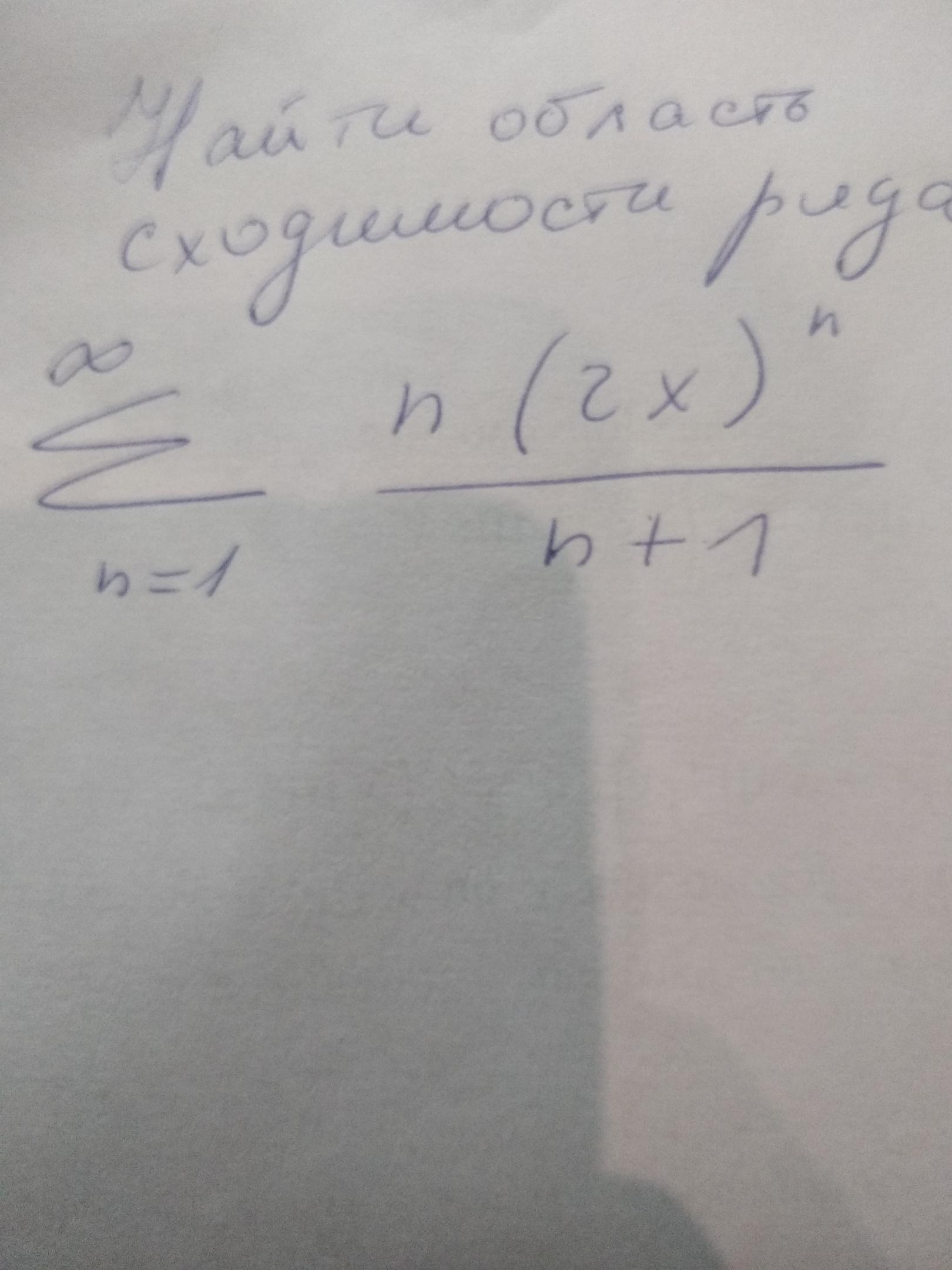
Ответы
Автор ответа:
1
Данный ряд расходится по необходимому признаку сходимости
Данный ряд расходится по признаку Лейбница, ряд знакочередующийся однако члены ряда не убывают по модулю. (Предел |a_n| не равен 0)
Соответственно область сходимости ряда:
Похожие вопросы
Предмет: Английский язык,
автор: politcom5
Предмет: Математика,
автор: tnastoyachay
Предмет: Алгебра,
автор: annaepiseva6
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: Алинка6324