Предмет: Алгебра,
автор: jefop33952
Может кто нибудь решить такое?
Приложения:
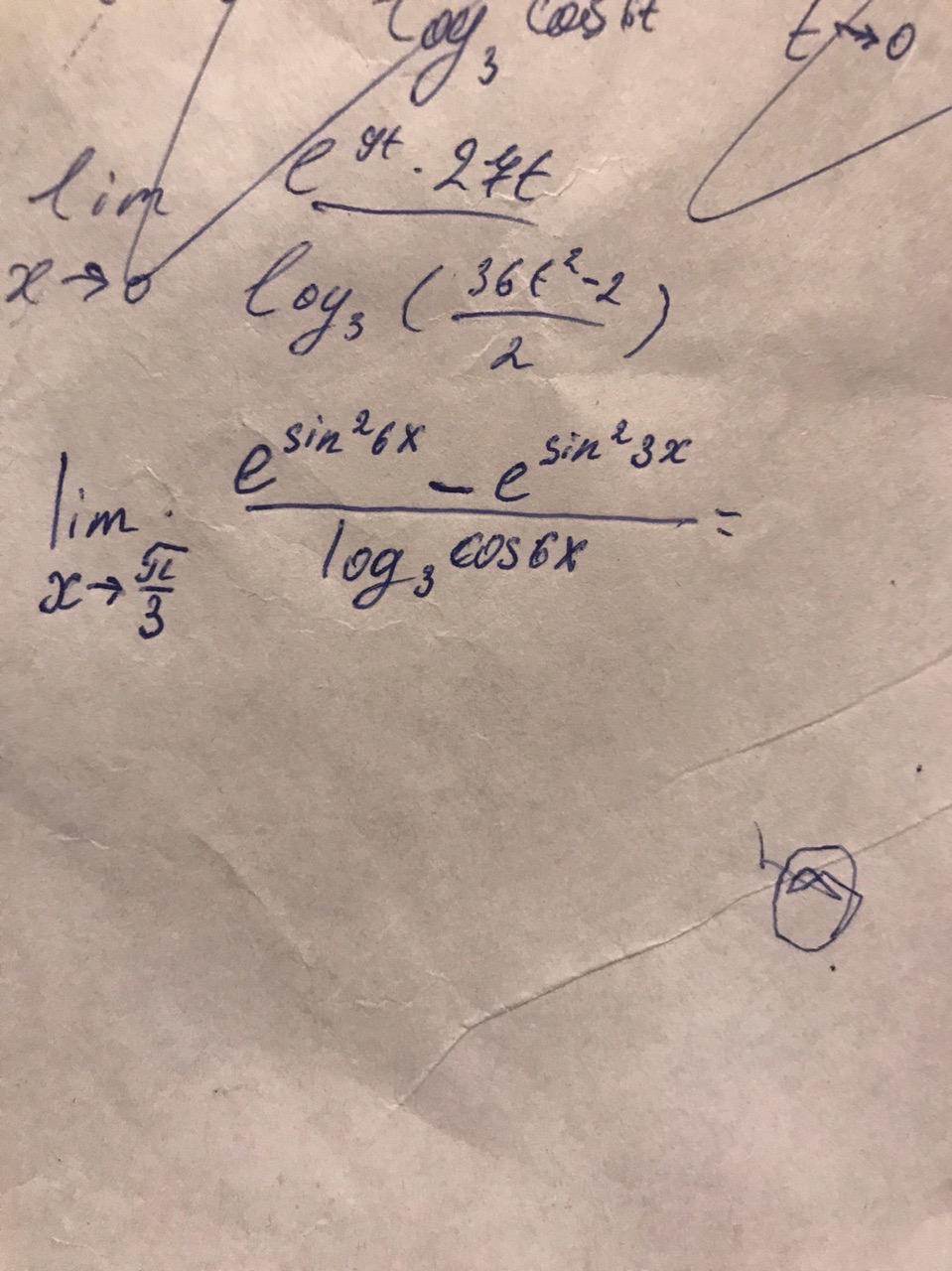
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: vladelec6479
Предмет: Математика,
автор: NASTIA3123
Предмет: Алгебра,
автор: markigorovic
Предмет: История,
автор: pineapple6969