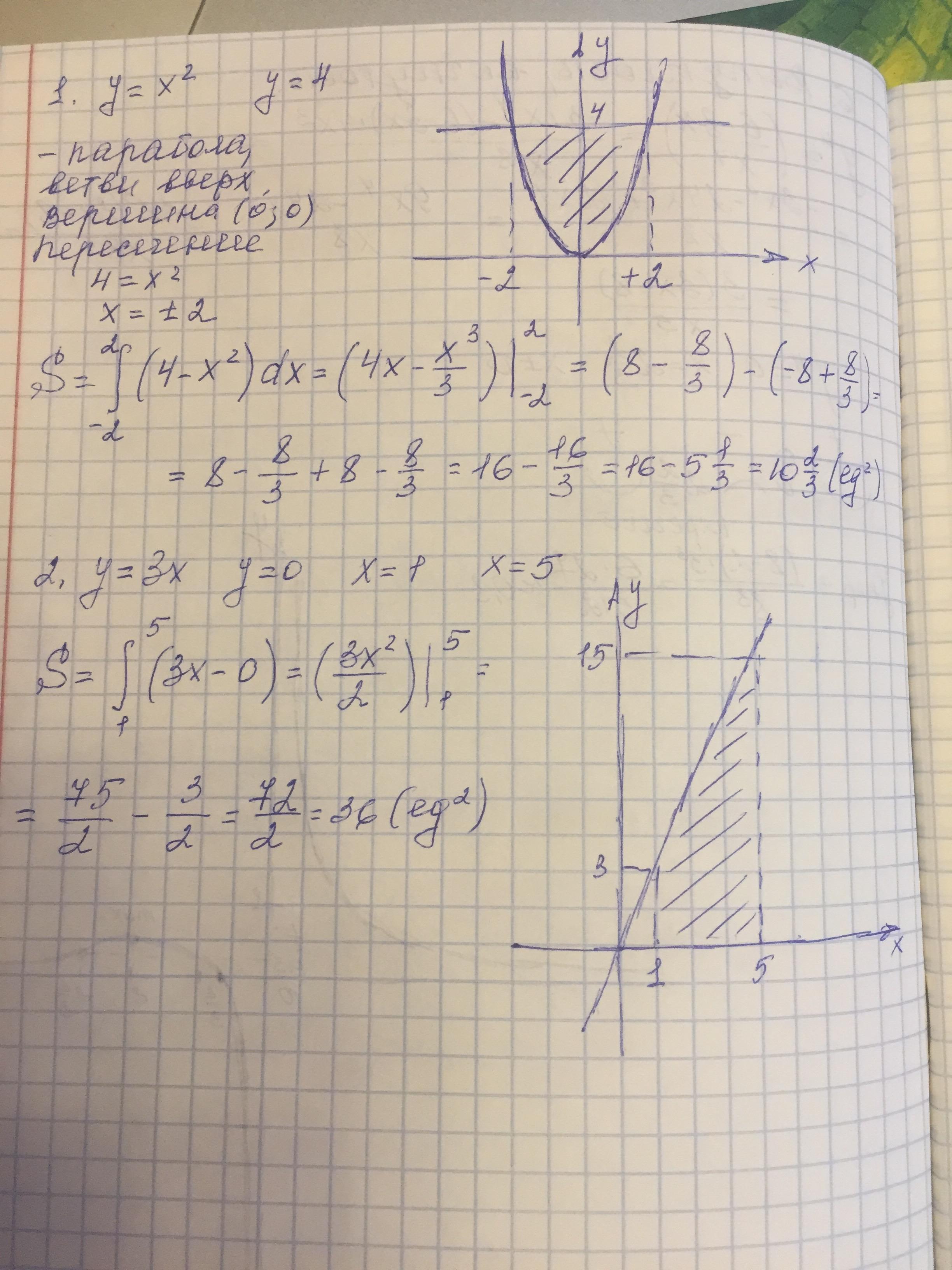
Вычислите площадь фигуры ограниченной графиками данной функции
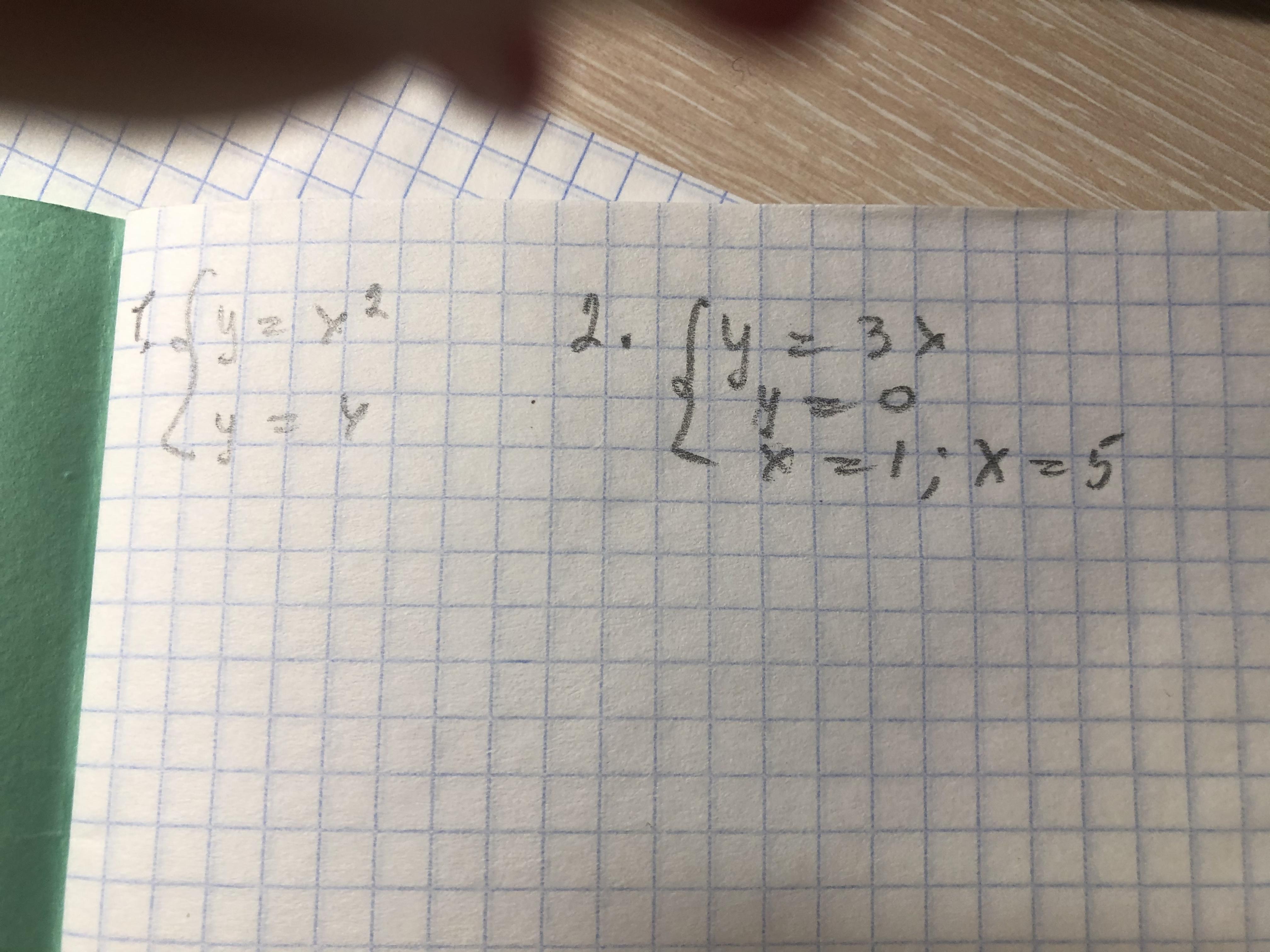
Ответы
Объяснение:
При решении этих задач самое важное узнать/понять какая функция из двух выше.
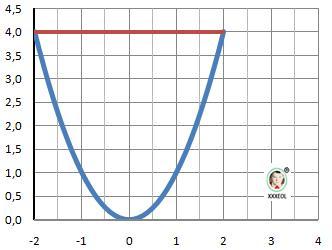
Задача 1. F(x) = 4 - прямая, Y(x) = x² - парабола
Рисунок к задаче в приложении.
Площадь это интеграл разности функций - верхней минус нижняя.
Находим пределы интегрирования - точки пересечения графиков: Y(x) = F(x)
х² = 4, x = √4 = ±2
a = -2, b= 2 - пределы интегрирования.
Пишем интеграл - площадь фигуры.
Вычисляем на пределах интегрирования.
S(b) = S(2) = 8 - 2 2/3 = 5 1/3
S(a) = S(-2) = -8 + 2 2/3 = -5 1/3
S = S(b)-S(a) = 5 1/3 - (-5 1/3) = 10 2/3 ед.²- площадь - ответ
Рисунок к задаче в приложении.
Задача 2. F(x) = 3*х и Y(x)=0 - функции,
a = 1, b = 5 - пределы интегрирования.
Площадь интеграл разности функций F(x)-Y(x).
ОТВЕТ: Площадь 36 ед.²

Ответ:
==============================
Объяснение: