Question

Приведите уравнение кривых к каноническому виду. Найдите центр, эксцентриситет, фокусы, асимптоты и директрисы. Сделайте чертеж:
а)16x^2 -9y^2 - 64x-54y-161=0
б)9x^2 +16y^2 +90x-32y-335=0

Answer 1

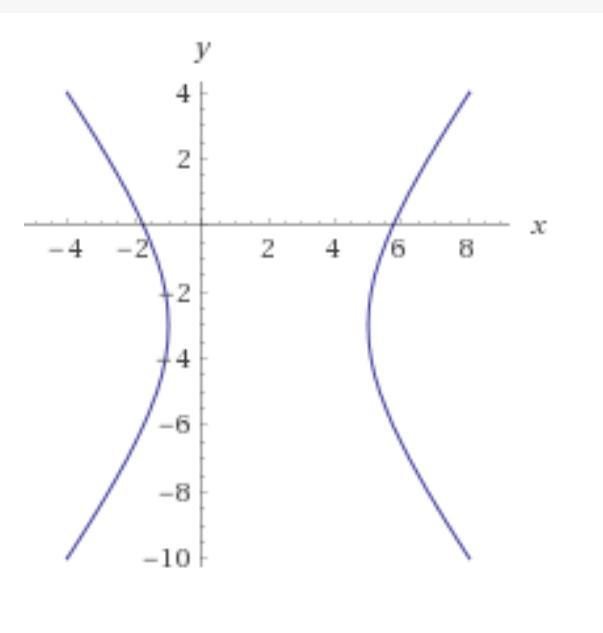
а) Дано уравнение 16x^2 - 9y^2 - 64x  -54y - 161 = 0.

Выделим полные квадраты.

16(x^2 - 4x + 4) - 16*4  - 9(y^2 + 6y + 9) + 9*9 - 161 = 0.

16(x - 2)² - 9(y + 3)²  = 144.

Разделим обе части уравнения на 144.

((x - 6)²/169) + ((y + 5)²/144)  = 1, или так:

(16(x - 2)²)/144) - (9(y + 3)²/144)  = 144/144.

(x - 2)²/9 + (y + 3)²/16  = 1 или в каноническом виде:

(x - 2)²/3² + (y + 3)²/4²  = 1.

Это уравнение гиперболы с центром в точке О(2; -3).

Полуоси гиперболы равны: а = 3, b = 4.

Подробнее параметры и график даны во вложениях.