Срочно помогите 62 балла
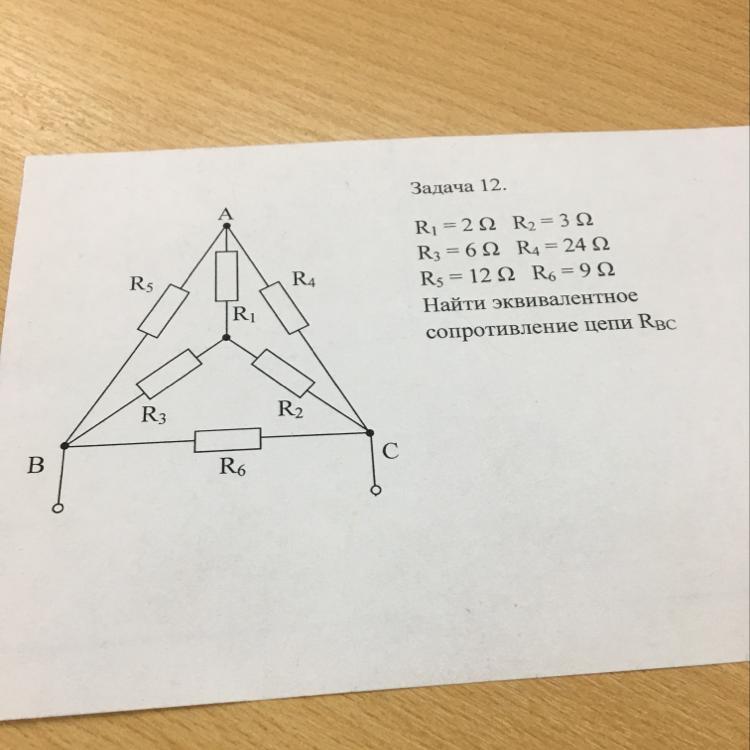
Ответы
Ответ:
Ом
Ом.
Объяснение:
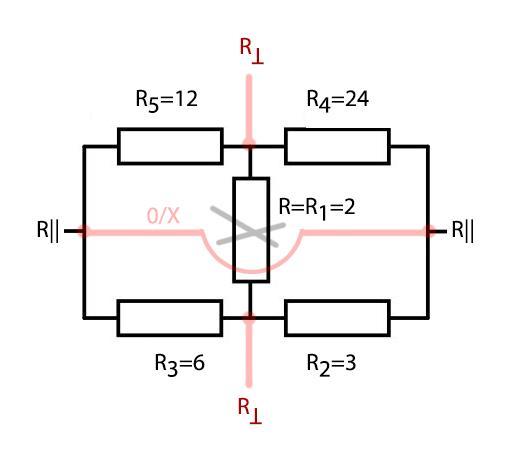
В другом варианте этой задачи уже было приведено классическое решение. Приведу здесь простой формальный способ, как разбираться с Ф-образными сцепками сопротивлений.
Для Ф-образной сцепки, представленной на приведённом внизу рисунке существует общая формула:
, где:
- сопротивление цепи, полученной из данной, выключением центрального сопротивления
,
- поперечное (вертикальное) сопротивление цепи, при выключенном центральном сопротивлении
без поперечного замыкания,
- вертикальное сопротивление цепи, при выключенном сопротивлении
и поперечном замыкании,
- сопротивление верхних резисторов, при использовании их, как пары параллельных,
- сопротивление нижних резисторов, при использовании их, как пары параллельных.
В нашем случае, Ф-образная сцепка состоит из резисторов: . Нижний
можно добавить в самом конце решения задачи, как параллельный.
Пара верхних резисторов Ф-образной сцепки: и
.
Пара нижних резисторов Ф-образной сцепки: и
.
- сопротивление параллельных резисторов по 36 Ом и 9 Ом:
Ом
Ом
Ом
Ом.
- сопротивление параллельных резисторов по 18 Ом и 27 Ом:
Ом
Ом
Ом
Ом.
- сопротивление параллельных резисторов по 12 Ом и 24 Ом:
Ом
Ом
Ом.
- сопротивление параллельных резисторов по 6 Ом и 3 Ом:
Ом
Ом
Ом.
- сопротивление последовательных резисторов по 8 Ом и 2 Ом:
Ом
Ом.
Подставляем всё в формулу для Ф-образной сцепки:
Ом
Ом
Ом
Ом
Ом.
Теперь найдём требуемое в задаче сопротивление, как параллельно включенные и Ф-образную сцепку:
Ом
Ом
Ом
Ом
Ом.