Ребят плиз помогите пожалуйста, дай вам бог здоровья.
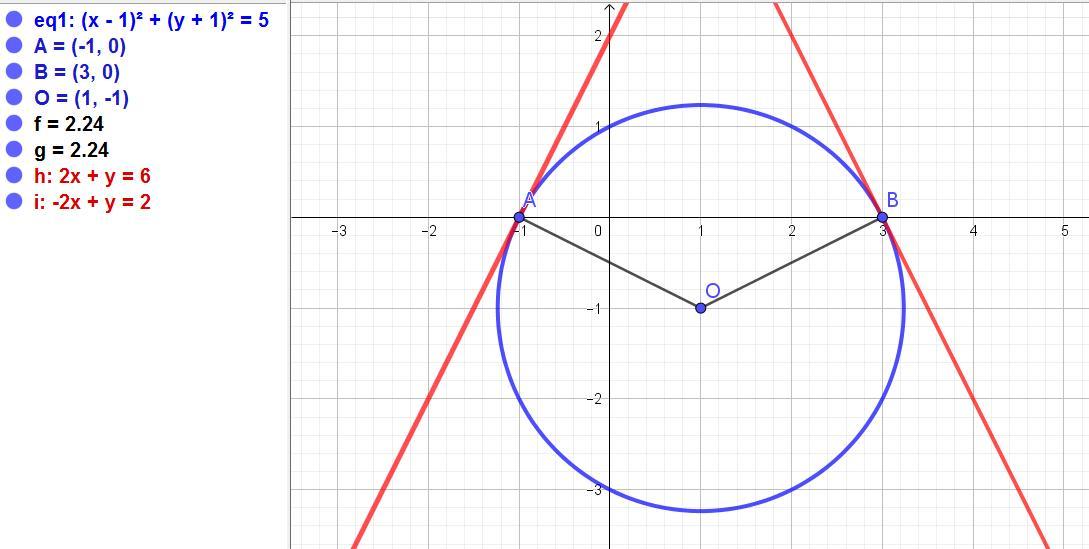
Составить уравнения касательных окружностей x^2+y^2-2x+2y-3=0 в точках её пересечения с осью х.
Ответы
Ответ: во вложении Пошаговое объяснение:

В точках пересечения окружности x²+y²-2x+2y-3=0 с осью Ох значение у = 0. Тогда x²-2x-3=0, Д = 4 - 4*(-3) = 16.
х₁ = (2 - 4)/2 = -1, х₂ = (2 + 4)/2 = 3.
Получили точки А(-1; 0) т В(3; 0).
Если выделить полные квадраты в уравнении, то получим:
(х - 1)² + (у + 1)² = 5.
Центр: точка О(1; -1).
Уравнение радиусов ОА и ОВ.
Векторы: ОА = ((-1 - 1); (0 - (-1)) = (-2; 1).
Векторы: ОВ = ((3 - 1); (0 - (-1)) = (2; 1).
Уравнение ОА: (х - 1)(-2) = (у + 1)/1, или у = (-1/2)х - (1/2).
Уравнение ОВ: (х - 1)(2) = (у + 1)/1, или у = (1/2)х - (3/2).
Уравнение касательной имеет угловой коэффициент к = -1/к(радиуса).
Уравнение касательной в точке А:
у = (-1/(-1/2))*х + в = 2х + в.
Для определения в подставим координаты точки А, через которую проходит касательная.
0 = 2*(-1) + в, отсюда в = 2.
Уравнение касательной в точке А: у = 2х + 2.
Аналогично находим в точке В: у = -2х + 6.
Можно находить уравнение касательной по формуле с производной, но в задании не оговорен этот способ.