Question

Решите пожалуйста
Завдання 10 - умова
17 нужно решить!

Answer 1

$1. AB=|\overrightarrow{AB}|=\sqrt{(-7-7)^2+(-4-(-5))^2}=\sqrt{(-14)^2+1^2}=\sqrt{197}$

2.

$M(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2} )\\ \\ M(\frac{-7-7}{2};\frac{-4+4}{2} )\\ \\ M(-7;0)$

Уравнение прямой:

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$

$\frac{x+7}{7+7}=\frac{y-0}{-5-0}\\ \\ \frac{y}{-5}=\frac{x+7}{14} \\ \\ y=-\frac{5(x+7)}{14}$

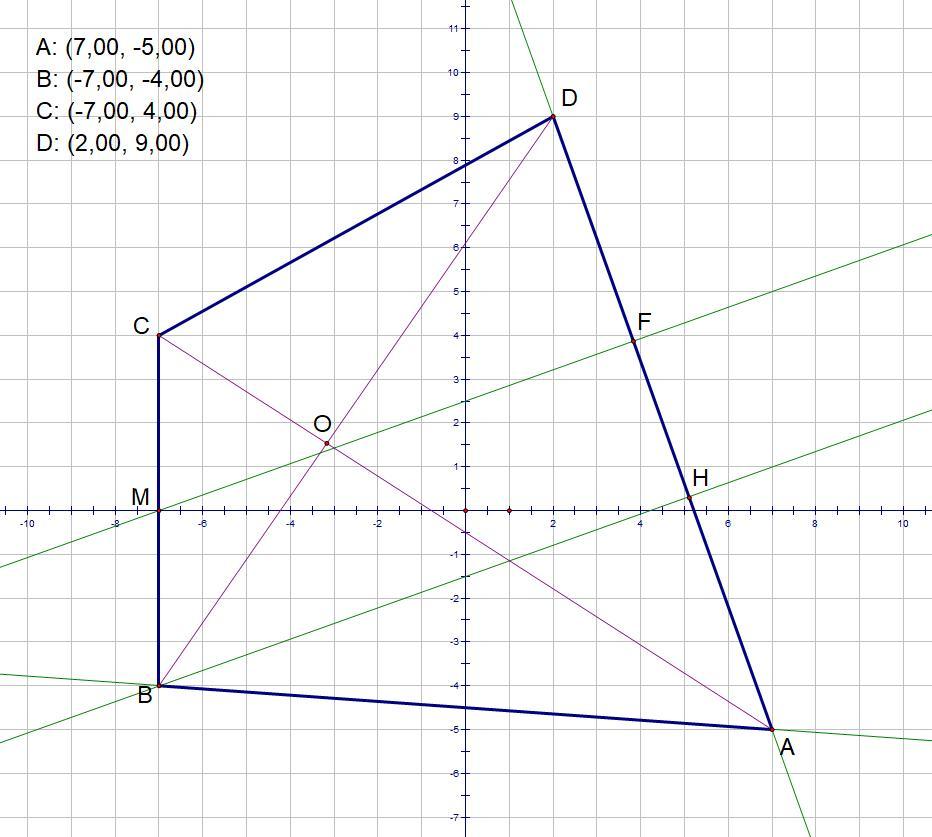
3. Пусть искомая прямая пересекает AD в точке H.

Сначала надо найти уравнение прямой AD:

$\frac{x-2}{7-2}=\frac{y-9}{-5-9}\\ \\ -\frac{14(x-2)}{5}=y-9\\ \\ y=-\frac{14(x-2)}{5}+9\\ \\ y=\frac{73-14x}{5}\\ \\ y=-2,8x+14,6$

Так как BH⊥AD, то коэффициенты k у них обратны и противоположны, то есть в уравнении прямой BH: y = k₁x + b₁    k₁ равно 5/14.

Известно, что B принадлежит прямой BH, значит её координаты обращают y = k₁x + b₁ в верное равенство. Подставим:

-4 = 5/14 * (-7) + b₁

b₁ = -1,5

Тогда уравнение BH имеет вид:

$y=\frac{5x}{14}-\frac{3}{2}$

4. Найдём уравнение прямой AB:

$\frac{x+7}{7+7}=\frac{y+4}{-5+4}\\ \\ \frac{x+7}{14}=-(y+4)\\ \\ y=- \frac{x+7}{14}-4\\ \\ y=-\frac{x}{14}-\frac{9}{2}$

Так как BH || AD, то коэффициенты k у них равны, то есть в уравнении искомой прямой y = k₂x + b₂    k₂ равно -1/14.

Известно, что D принадлежит искомой прямой, значит её координаты обращают y = k₂x + b₂ в верное равенство. Подставим:

9 = -1/14 * 2 + b₂

b₂ = 64/7

Тогда уравнение искомой прямой имеет вид:

$y=-\frac{x}{14}+\frac{64}{7}$

5.

$\overrightarrow{BA}=(7+7;-5+4)=(14;-1)\\ \\ \overrightarrow{BC}=(-7+7;4+4)=(0;8)\\ \\ |\overrightarrow{BC}|=\sqrt{0^2+8^2}=\sqrt{64}=8\\\\ |\overrightarrow{BA}|=\sqrt{197} \\ \\ cos\angle B=\frac{\overrightarrow{BC}\cdot\overrightarrow{BA}}{|\overrightarrow{BC}|\cdot|\overrightarrow{BA}|} =\frac{0\cdot14+8\cdot(-1)}{8\cdot\sqrt{197}}=-\frac{1}{\sqrt{197}}\\ \\ \angle B=arccos(-\frac{1}{\sqrt{197}})$

6. Расстояние от точки до прямой -- это перпендикуляр, проведенной из этой точки к данной прямой. Пусть такая прямая пересекает AD в точке F.

Для вычисления расстояния MF, необходимы координаты F.

Найдём сначала уравнение прямой MF. Так как MF || BH, то коэффициенты k у них равны, то есть в уравнении искомой прямой y = k₃x + b₃    k₃ равно 5/14.

Известно, что M принадлежит искомой прямой, значит её координаты обращают y = k₃x + b₃ в верное равенство. Подставим:

0 = 5/14 * (-7) + b₃

b₃ = 5/2

Тогда уравнение прямой MF имеет вид:

$y=\frac{5x}{14}+\frac{5}{2}$

Пересечение прямых MF и AD есть точка F. Составим систему уравнений и найдём координаты точки F:

$\left \{ {{y=\frac{-14x}{5}+\frac{73}{5}, } \atop {y=\frac{5x}{14}+\frac{5}{2}} \right. \\ \\ \left \{ {{x=\frac{847}{221}, } \atop {y=\frac{855}{221} }} \right. \\ \\ F(\frac{847}{221};\frac{855}{221})$

Теперь находим искомое расстояние MF:

$MF=|\overrightarrow{MF}|=\sqrt{(\frac{847}{221}+7)^2+(\frac{855}{221}-0)^2}=\sqrt{\frac{29241}{221}}=\frac{171}{\sqrt{221}}$

8.  Площадь произвольного четырёхугольника находится по формуле

$S=d_1\cdot d_2\cdot sin\alpha$

где d₁, d₂ -- диагонали четырёхугольника, а альфа -- угол между ними.

Найдём длины диагоналей AC и DB, а также косинус угла между ними (из него найдём синус угла)

$\overrightarrow{AC}=(7+7;-5-4)=(14;-9)\\ \\ \overrightarrow{DB}=(-7-2;-4-9)=(-9;-13)\\ \\ |\overrightarrow{AC}|=\sqrt{14^2+(-9)^2}=\sqrt{196+81}=\sqrt{277}\\\\ |\overrightarrow{DB}|=\sqrt{(-9)^2+(-13)^2}=\sqrt{81+169}=\sqrt{250}=5\sqrt{10} \\ \\ cos\angle \alpha =\frac{\overrightarrow{AC}\cdot\overrightarrow{DB}}{|\overrightarrow{AC}|\cdot|\overrightarrow{DB}|} =\frac{14\cdot(-9)+(-9)\cdot(-13)}{\sqrt{277}\cdot5\sqrt{10}}=\frac{-9}{5\sqrt{2770} }$

$sin\angle \alpha=\sqrt{1-cos^2\angle \alpha}=\sqrt{1-(\frac{-9}{5\sqrt{2770} })^2}=\sqrt{1-\frac{81}{25\cdot2770} }=\sqrt{\frac{69169}{25\cdot2770}} }=\frac{263}{5\sqrt{2770} }$

Подставим найденные значения в формулы площади:

$S=AC\cdot DB\cdot sin\angle\alpha=\sqrt{277}\cdot5\sqrt{10} \cdot\frac{263}{5\sqrt{277}\sqrt{10}  }=263$